Multinomial Logit regression
- 1. Preparation
- 2. Download the data
- 3. Load the data
- 4. Distribution of DV
- 5. recode DV
- 6. Distribution of IV
- 7. country name
- 8. Examine your data
- 10. multinomial logit (SQ as the baseline)
- 11. Create a new variable to be used as the DV
- 12. Compare this with the original
- 13. Make it a factor
- 14. Estimate the same m-logit model with Neg as the baseline
- 16. Combined table
- 17. effects based on fit.0
- 18. effects based on fit.1
- 19. Make the IDV a factor
- 20. Estimate a m-logit model again, and compare
- 21. Substantive effects
- 22. plot the effects
- 23. Replication
1. Preparation
rm(list = ls()) # delete everything in the memory
library(foreign) # for read.dta
library(ggplot2) # for graphics
library(stargazer) # Regression table
library(effects) # for effect
library(nnet) # for multinom
library(countrycode) # for country codeNote: Starting from today, you need to learn how to describe your data, model, and design in your empirical section of your research paper. Make everything transparent and easy to understand.
2. Download the data
We will replicate the main results of Huth, Crocco, & Appel’s (2005) analysis of territorial dispute outcome. The article and the data set are available on Blackboard.
Download the replication data set (isq dvsqb.dta.dta) from Blackboard, and save it to a location where you can access from.
4. Distribution of DV
dvsqb is the dependent variable that measures an outcome of a territorial dispute for a given dispute-month. This is essentially a foreign policy choice made by the “challenger” in a territorial dispute in a given month. It takes three values, 0 (maintain status quo / do nothing), 1 (call for negotiation), and 2 (use or threaten to use military force). Use the table function to find the distribution of this variable.
table(td$dvsqb)##
## 0 1 2
## 2459 1140 2415. recode DV
We will recode this variable and make it into a factor variable. We do this because doing so will make the subsequent interpretation process easier (the stargazer table will automatically have intuitive labels if we do this).
Let’s create a new variable named dvsqb.cat that has three values, “SQ”, “Neg”, and “Mil” corresponding to the three numerical values, 0, 1, and 2. Once you create it, make sure it has been created correctly by taking a look at the distribution of the new variable.
td$dvsqb.cat <- factor(td$dvsqb,
label = c("SQ","Neg", "Mil"))
table(td$dvsqb.cat)##
## SQ Neg Mil
## 2459 1140 241Compare this with the original. Check if they are the same.
table(td$dvsqb.cat, td$dvsqb)##
## 0 1 2
## SQ 2459 0 0
## Neg 0 1140 0
## Mil 0 0 2416. Distribution of IV
slc3b is the main independent variable, which measures whether or not the challenger has a clear legal advantage in its territorial claim (= 1) or not (= 0). The value of 0 means either one of the following: (1) both the challenger and the target has a legitimate legal claim (maybe the challenger has an advantage based on some treaty, whereas the target has an advantage based on some customary international law), (2) only the target has a legitimate claim, (3) neither the challenger nor target has a legitimate legal claim (legal precedence is unclear with respect to the claim). Find the distribution of this variable.
table(td$slc3b)##
## 0 1
## 3671 1697. country name
The cowcntry variable records the COW country code of the challenger state, whereas the opponent variable is for the target. Using the countrycode function from the countrycode package, convert these variables into country names.
td $ challenger <- countrycode(td$cowcntry, origin = "cown", destination = "country.name")## Warning: Some values were not matched unambiguously: 260td $ target <- countrycode(td$opponent, origin = "cown", destination = "country.name")8. Examine your data
dispute-dyad with slc3b==1
List up all the challenger-target pairs where the challenger has a clear legal advantage. The output should look like the one on slide 13. That is, there will be 14 unique country pairs where slc3b is equal to 1.
unique(td[td $ slc3b == 1, c("challenger", "target")])## challenger target
## 7 Botswana Namibia
## 532 Chad Libya
## 745 Egypt Israel
## 809 Iran United Kingdom
## 1610 Argentina Uruguay
## 2037 Nicaragua United States
## 2184 Paraguay Argentina
## 2321 Afghanistan Russia
## 3298 Portugal Indonesia
## 3451 Cyprus Turkey
## 3477 Czechoslovakia Hungary
## 3519 France Italy
## 3683 Romania Hungary
## 3791 <NA> Francedispute-dyad with slc3b==0
List up all the challenger-target pairs where the challenger does not have a clear legal advantage. The output is quite long. A subset of this list is shown on slide 14. There will be 165 unique country pairs where slc3b is equal to 0.
unique(td[td$slc3b == 0, c("challenger", "target")])## challenger target
## 1 Benin Niger
## 18 United Kingdom Ethiopia
## 28 Comoros France
## 54 Ethiopia United Kingdom
## 55 Ethiopia Kenya
## 79 Ethiopia Sudan
## 114 Gabon Equatorial Guinea
## 115 Ghana Côte d’Ivoire
## 116 Ghana France
## 125 Ghana Togo
## 134 Somalia Ethiopia
## 139 Italy Ethiopia
## 183 Lesotho South Africa
## 217 Liberia France
## 247 Madagascar France
## 266 Malawi Zambia
## 272 Mali Mauritania
## 275 Mali Burkina Faso
## 306 Mauritius France
## 333 Mauritius United Kingdom
## 355 Morocco Mauritania
## 356 Morocco France
## 369 Namibia South Africa
## 372 Nigeria Cameroon
## 409 Somalia Kenya
## 417 Somalia United Kingdom
## 433 Somalia France
## 451 Togo Ghana
## 493 Uganda Tanzania
## 499 Congo - Kinshasa Zambia
## 521 Eritrea Ethiopia
## 524 Niger Benin
## 554 Iraq Saudi Arabia
## 590 Yemen People's Republic Saudi Arabia
## 593 United Kingdom Saudi Arabia
## 596 Yemen Saudi Arabia
## 649 United Arab Emirates Saudi Arabia
## 678 Egypt United Kingdom
## 688 Egypt Sudan
## 741 Egypt Israel
## 780 Eritrea Yemen
## 785 Iran United Kingdom
## 834 Iran Iraq
## 863 Iran Saudi Arabia
## 883 Iraq United Kingdom
## 886 Iraq Kuwait
## 940 Iraq Iran
## 955 Jordan Israel
## 997 Libya France
## 998 Libya Chad
## 1017 Mauritania Spain
## 1035 Morocco Algeria
## 1052 Morocco Spain
## 1119 Yemen Arab Republic United Kingdom
## 1120 Yemen Arab Republic Yemen People's Republic
## 1157 Oman Saudi Arabia
## 1175 Qatar Bahrain
## 1204 Kuwait Saudi Arabia
## 1205 Saudi Arabia Kuwait
## 1206 Saudi Arabia United Kingdom
## 1260 Saudi Arabia Jordan
## 1284 Saudi Arabia Oman
## 1337 Saudi Arabia Qatar
## 1338 Russia Iran
## 1350 Russia Turkey
## 1360 Yemen Oman
## 1361 Yemen People's Republic Oman
## 1371 Syria Israel
## 1424 Tunisia France
## 1432 Tunisia Algeria
## 1444 United Arab Emirates Iran
## 1475 United Arab Emirates Oman
## 1495 Lebanon Israel
## 1496 Argentina United Kingdom
## 1557 Argentina Chile
## 1642 Bolivia Chile
## 1696 Cuba United States
## 1738 Ecuador Peru
## 1794 El Salvador Honduras
## 1840 Guatemala United Kingdom
## 1846 Guatemala Belize
## 1897 Haiti United States
## 1953 Honduras United States
## 1981 Mexico United States
## 1998 Nicaragua Colombia
## 2020 Nicaragua Honduras
## 2039 Suriname Guyana
## 2040 Netherlands United Kingdom
## 2042 Netherlands Guyana
## 2097 Netherlands France
## 2099 Suriname France
## 2153 Panama United States
## 2185 United States Canada
## 2214 Venezuela Guyana
## 2221 Venezuela United Kingdom
## 2263 Afghanistan Pakistan
## 2323 India France
## 2326 United Kingdom France
## 2333 Cambodia Vietnam
## 2362 Cambodia Thailand
## 2372 China Afghanistan
## 2391 China Bhutan
## 2416 China United Kingdom
## 2456 China India
## 2478 China Myanmar (Burma)
## 2494 China Vietnam
## 2495 China Republic of Vietnam
## 2505 China France
## 2559 China Japan
## 2613 China Nepal
## 2626 China Kazakhstan
## 2628 China Kyrgyzstan
## 2636 China Mongolia
## 2654 China Pakistan
## 2670 China Portugal
## 2701 China Russia
## 2774 China Tajikistan
## 2783 France Thailand
## 2784 India China
## 2831 India Pakistan
## 2857 India Portugal
## 2872 Indonesia Netherlands
## 2884 Indonesia Malaysia
## 2906 Japan Russia
## 2967 Malaysia China
## 2990 Malaysia Singapore
## 3012 North Korea South Korea
## 3072 Vietnam Republic of Vietnam
## 3086 Pakistan India
## 3153 Bangladesh India
## 3210 Portugal India
## 3223 Papua New Guinea Australia
## 3226 Philippines China
## 3257 Philippines Malaysia
## 3321 South Korea Japan
## 3377 Thailand France
## 3380 Thailand Cambodia
## 3382 Thailand Laos
## 3403 Vanuatu France
## 3422 Brunei Malaysia
## 3438 Austria Italy
## 3440 Croatia Slovenia
## 3478 German Democratic Republic United States
## 3502 Estonia Russia
## 3509 Finland Russia
## 3511 France United Kingdom
## 3520 Greece Albania
## 3547 Greece Bulgaria
## 3548 Greece Cyprus
## 3561 Greece United Kingdom
## 3570 Ireland United Kingdom
## 3627 Italy Yugoslavia
## 3659 Latvia Russia
## 3669 Netherlands Belgium
## 3685 Slovakia Czechia
## 3687 Spain United Kingdom
## 3746 Turkey United Kingdom
## 3753 <NA> Czechoslovakia
## 3773 <NA> German Democratic Republic
## 3793 <NA> Poland
## 3811 <NA> Netherlands
## 3816 Yugoslavia Greece
## 3818 Yugoslavia Croatia
## 3826 Yugoslavia North Macedonia
## 3831 Turkey Greece10. multinomial logit (SQ as the baseline)
Using the multinom function from the nnet package, estimate a multinomial logit model that controls for slc3b. Then, create a stargazer table. The results should look exactly like the one on the slide.
library(nnet)
fit.0 <- multinom(dvsqb.cat ~ slc3b, data = td)## # weights: 9 (4 variable)
## initial value 4218.671188
## iter 10 value 3137.766235
## final value 3137.761465
## convergedweights refers to the refers to the optional case weights in fitting. They adjust the importance of each observation during model fitting, which may be useful in situations where certain observations are more reliable than others or when dealing with imbalanced datasets.
initial value refers to the starting values used for the parameters (coefficients) in the optimization algorithm that multinom uses to fit the model.
final value refers to the end values in the optimization algorithm
stargazer(fit.0, type = "text")##
## ==============================================
## Dependent variable:
## ----------------------------
## Neg Mil
## (1) (2)
## ----------------------------------------------
## slc3b 0.717*** -0.030
## (0.162) (0.376)
##
## Constant -0.804*** -2.322***
## (0.037) (0.069)
##
## ----------------------------------------------
## Akaike Inf. Crit. 6,283.523 6,283.523
## ==============================================
## Note: *p<0.1; **p<0.05; ***p<0.01We will estimate the same model but with a different baseline
11. Create a new variable to be used as the DV
As I explained in the lecture, this result assumes the Status Quo outcome as the baseline. To estimate the same model using the Negotiation outcome as the baseline, we have to recode the dependent variable. Create a new variable named dvsqb.base1 that is coded as follows:
td$dvsqb.base1 <- td$dvsqb
td$dvsqb.base1[td$dvsqb == 0] <- 312. Compare this with the original
Run table(td$dvsqb, td$dvsqb.base1) to compare the newly created variable with the original. Make sure that the dvsqb.base1 variable has been correctly created.
table(td $ dvsqb, td $ dvsqb.base1)##
## 1 2 3
## 0 0 0 2459
## 1 1140 0 0
## 2 0 241 0We see that 0 (SQ) is replaced by the number 3. A new order is created.
table(td$dvsqb.cat)##
## SQ Neg Mil
## 2459 1140 24113. Make it a factor
Create a factor variable that has “SQ”, “Neg”, and “Mil” as values. Name this new variable dvsqb.cat.b1. Be extra careful about the ordering of the labels. That is, keep in mind that the values are now ordered as “Neg”, “Mil”, “SQ”. You have to make some necessary adjustment when using the labels option.
Run table(td$dvsqb.cat.b1) to make sure that you have created this variable correctly. Does the Neg category have 1140 observations? Does the SQ category have 2459 observations? Are they ordered in the correct way?
td $ dvsqb.cat.b1 <- factor(td $ dvsqb.base1, label = c("Neg", "Mil", "SQ"))
table(td $ dvsqb.cat.b1)##
## Neg Mil SQ
## 1140 241 245914. Estimate the same m-logit model with Neg as the baseline
Estimate the same multinomial logit model but with Neg as the baseline, then create a stargazer table. The table should look like the one on the slide.
fit.1 <- multinom(dvsqb.cat.b1 ~ slc3b, data = td)## # weights: 9 (4 variable)
## initial value 4218.671188
## iter 10 value 3138.554477
## final value 3137.761465
## convergedstargazer(fit.1, type = "text")##
## ==============================================
## Dependent variable:
## ----------------------------
## Mil SQ
## (1) (2)
## ----------------------------------------------
## slc3b -0.747** -0.717***
## (0.378) (0.162)
##
## Constant -1.518*** 0.804***
## (0.072) (0.037)
##
## ----------------------------------------------
## Akaike Inf. Crit. 6,283.523 6,283.523
## ==============================================
## Note: *p<0.1; **p<0.05; ***p<0.0116. Combined table
Create another stargazer table that combines the estimates from the first estimation and the second estimation. The table should look like the one on slide 20. Notice how the fourth column is redundant, for the estimates are exactly the same as the first column except for the signs.
stargazer(fit.0, fit.1, type = "text",
column.labels = c("Neg v SQ", "Mil v SQ", "Mil v Neg", "SQ v Neg"))##
## =========================================================
## Dependent variable:
## ---------------------------------------
## Neg Mil SQ
## Neg v SQ Mil v SQ Mil v Neg SQ v Neg
## (1) (2) (3) (4)
## ---------------------------------------------------------
## slc3b 0.717*** -0.030 -0.747** -0.717***
## (0.162) (0.376) (0.378) (0.162)
##
## Constant -0.804*** -2.322*** -1.518*** 0.804***
## (0.037) (0.069) (0.072) (0.037)
##
## ---------------------------------------------------------
## Akaike Inf. Crit. 6,283.523 6,283.523 6,283.523 6,283.523
## =========================================================
## Note: *p<0.1; **p<0.05; ***p<0.0117. effects based on fit.0
Calculate the substantive effects of the slc3b variable using the estimation results from Task 10. The output should look like the one on slide 23.
effect(term = "slc3b", mod = fit.0)##
## slc3b effect (probability) for SQ
## slc3b
## 0 0.2 0.5 0.8 1
## 0.6469627 0.6195382 0.5756415 0.5290925 0.4970415
##
## slc3b effect (probability) for Neg
## slc3b
## 0 0.2 0.5 0.8 1
## 0.2895669 0.3200413 0.3687165 0.4202179 0.4556212
##
## slc3b effect (probability) for Mil
## slc3b
## 0 0.2 0.5 0.8 1
## 0.06347044 0.06042046 0.05564210 0.05068957 0.0473372818. effects based on fit.1
Calculate the substantive effects of the slc3b variable using the estimation results from Task 15. The output should be almost identical to the one you obtained above, except for the ordering of the outcomes. That is, the first one lists the outcome probabilities for SQ, Neg, Mil in this order, whereas the second one lists Neg, Mil, and SQ in this order. However, if you compare the probabilities for the same outcome, the estimates should be almost identical (up to the fourth or fifth decimal point).
effect(term = "slc3b", mod = fit.1)##
## slc3b effect (probability) for Neg
## slc3b
## 0 0.2 0.5 0.8 1
## 0.2895670 0.3200416 0.3687171 0.4202188 0.4556224
##
## slc3b effect (probability) for Mil
## slc3b
## 0 0.2 0.5 0.8 1
## 0.06347074 0.06042051 0.05564181 0.05068899 0.04733654
##
## slc3b effect (probability) for SQ
## slc3b
## 0 0.2 0.5 0.8 1
## 0.6469623 0.6195379 0.5756411 0.5290922 0.497041119. Make the IDV a factor
As I pointed out in the lecture, we don’t want to have outcome probabilities for some “unrealistic” values. That is slc3b takes only two values, 0 or 1 and so it never takes values such as 0.2, 0.4, 0.6, or 0.8. Yet, R calculates outcome probabilities for these cases because R doesn’t realize that this is a binary variable. To make R realize this, we should have made slc3b into a factor variable and used it instead when estimating multinomial logit models. Let’s do this now. Create a new variable that is a factor variable that takes a value “No” if slc3b is 0 and “Yes” if slc3b is 1
td $ slc3b.fac <- factor(td $ slc3b, label = c("No", "Yes"))20. Estimate a m-logit model again, and compare
Estimate a multinomial logit model again. Compare the estimates with the one that includes the original slc3b to make sure that you get the same estimates.
fit.f0 <- multinom(dvsqb.cat ~ slc3b.fac, data = td)## # weights: 9 (4 variable)
## initial value 4218.671188
## iter 10 value 3137.766235
## final value 3137.761465
## convergedstargazer(fit.0, fit.f0, type = "text")##
## =========================================================
## Dependent variable:
## ---------------------------------------
## Neg Mil Neg Mil
## (1) (2) (3) (4)
## ---------------------------------------------------------
## slc3b 0.717*** -0.030
## (0.162) (0.376)
##
## slc3b.facYes 0.717*** -0.030
## (0.162) (0.376)
##
## Constant -0.804*** -2.322*** -0.804*** -2.322***
## (0.037) (0.069) (0.037) (0.069)
##
## ---------------------------------------------------------
## Akaike Inf. Crit. 6,283.523 6,283.523 6,283.523 6,283.523
## =========================================================
## Note: *p<0.1; **p<0.05; ***p<0.0121. Substantive effects
Calculate the substantive effects based on the new model. Make sure that the outputs are similar to the previous one, except that the new one doesn’t have outcome probabilities for “unrealistic” values. (This makes a difference when we plot them. If we plot the previous one, the graph will contain “unrealistic” values and we don’t want that.)
eff.0 <- effect(term = "slc3b.fac", mod = fit.f0)
eff.0##
## slc3b.fac effect (probability) for SQ
## slc3b.fac
## No Yes
## 0.6469627 0.4970415
##
## slc3b.fac effect (probability) for Neg
## slc3b.fac
## No Yes
## 0.2895669 0.4556212
##
## slc3b.fac effect (probability) for Mil
## slc3b.fac
## No Yes
## 0.06347044 0.04733728plot(Effect("slc3b.fac",fit.f0)) 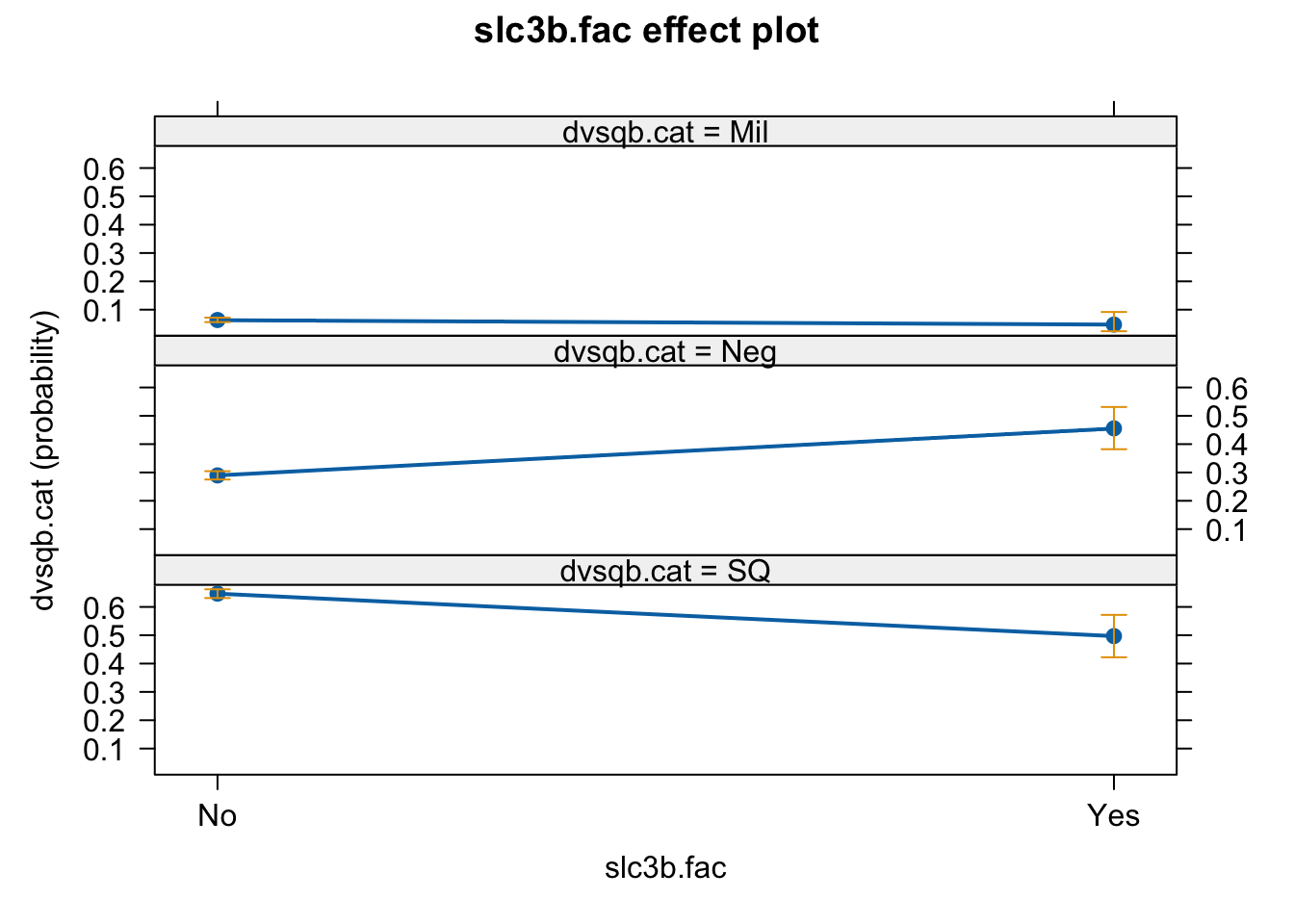
22. plot the effects
Plot the substantive effects. The graph should look similar to the one on slide 26.
# pdf(file = "mleff1.pdf", width = 10, height = 7)
plot(eff.0, rescale.axis = FALSE, style = "stacked",
main = "Effect of legal advantage",
xlab = "Challenger has a legal advantage",
ylab = "Outcome probabilities")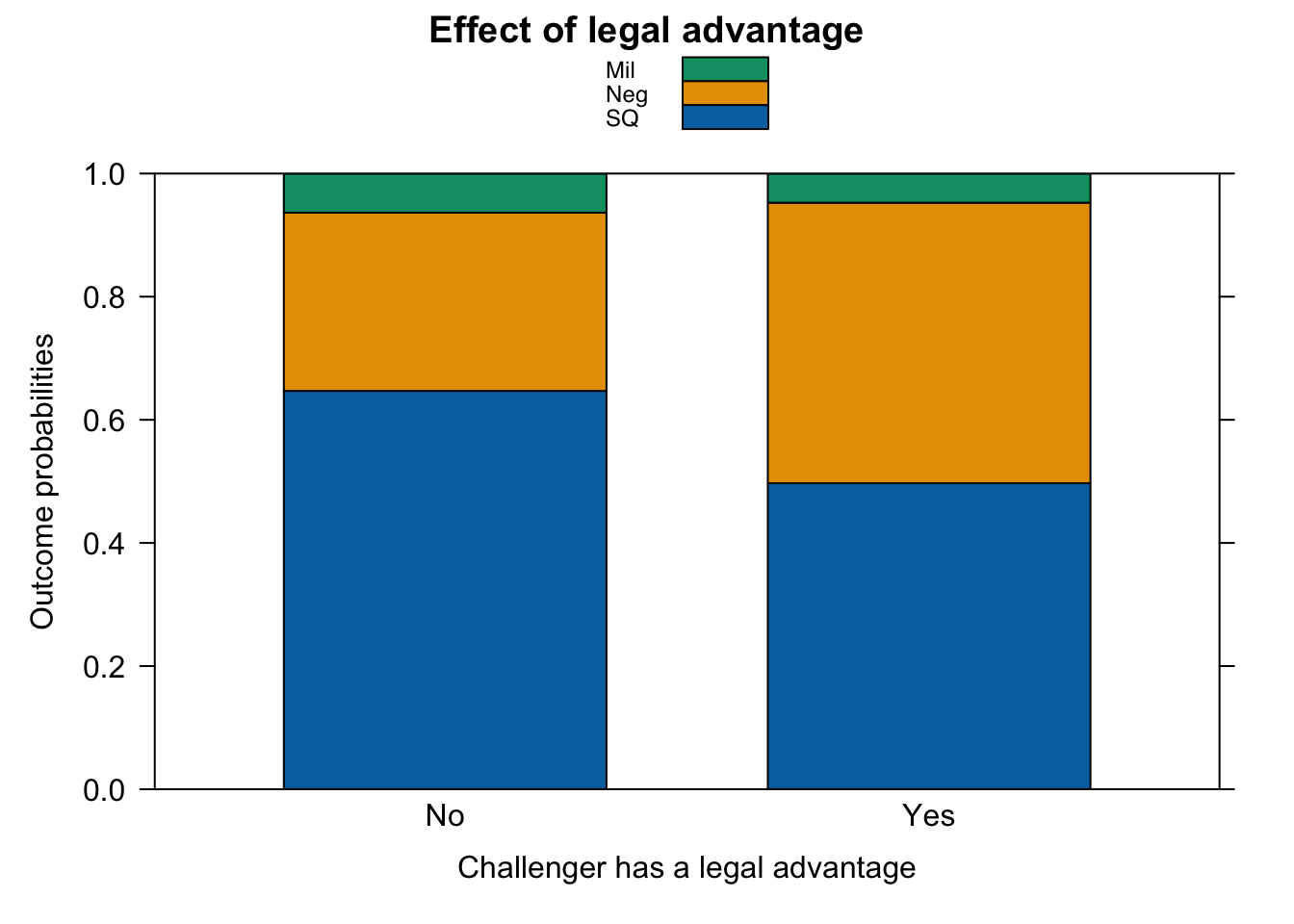
# dev.off()Here I use the marginaleffects package because it’s the only one so far support effect plots with CIs with the m-logit model. More information about the pacakge can be found here.
# remotes::install_github("vincentarelbundock/marginaleffects")
library(marginaleffects)
fit.f0 <- multinom(dvsqb.cat.b1 ~ slc3b, data = td)## # weights: 9 (4 variable)
## initial value 4218.671188
## iter 10 value 3138.554477
## final value 3137.761465
## convergedplot_predictions(
fit.f0,
type = "probs",
condition = "slc3b") +
facet_wrap(~group) +
theme_bw() +
ggtitle(element_blank()) +
xlab("Strong Legal Claim by Challenger") + ylab("Pr(Outcome)") +
labs(title = "Effect Plot") +
theme(plot.title = element_text(hjust = 0.5)) 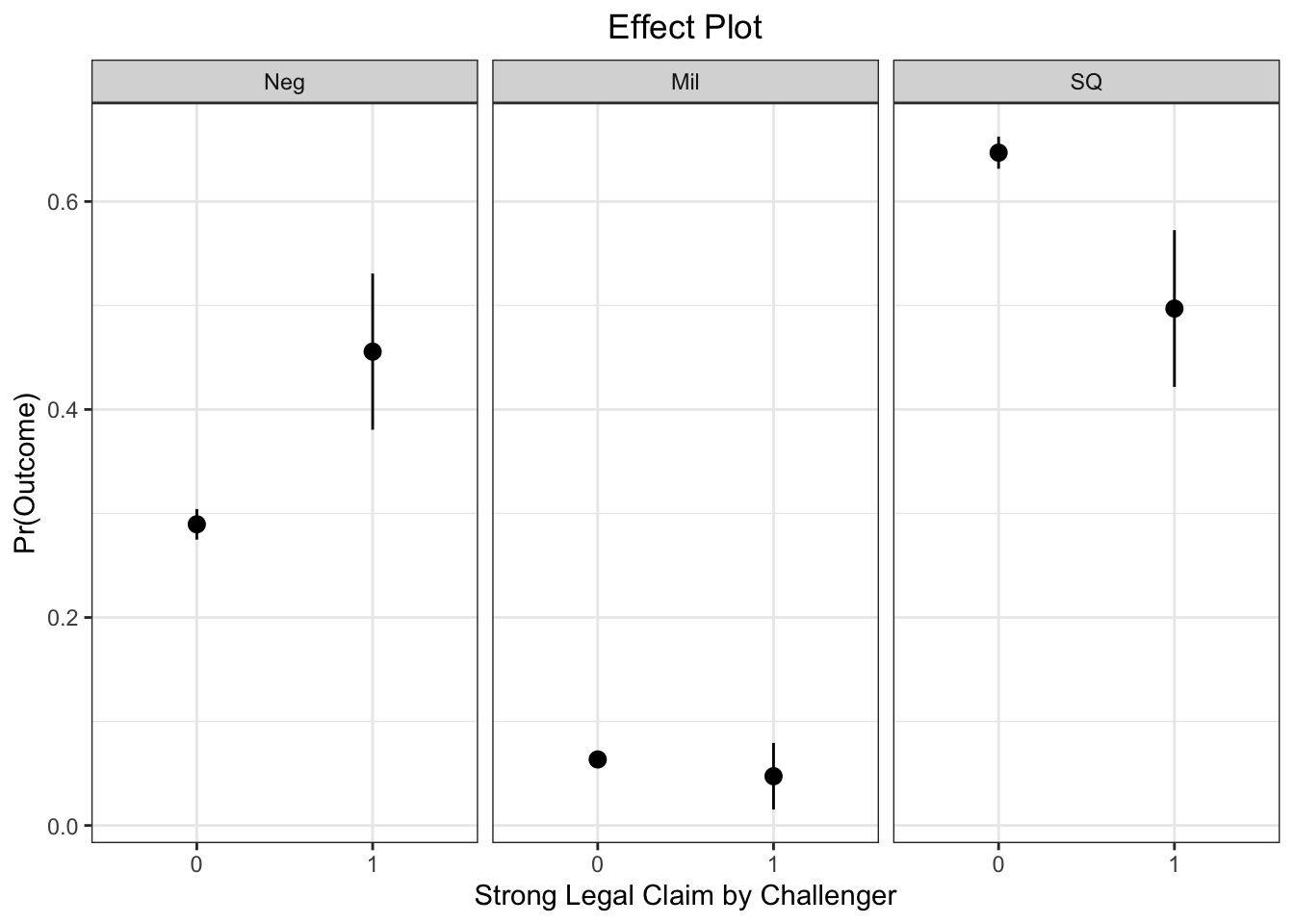
23. Replication
Full models: include other independent variables
Replicate Table 2 on page 27 of the article as closely as possible. If you can produce something that is close to the one on slide 29, that’s fine. Note that the authors use what’s called “robust” standard errors whereas we don’t, so the standard errors will be somewhat different.
# The authors use Mil as the baseline, so let's do this
td $ dvsqb.base2 <- td $ dvsqb
td $ dvsqb.base2[td $ dvsqb == 2] <- -1
table(td $ dvsqb.base2)##
## -1 0 1
## 241 2459 1140table(td $ dvsqb, td $ dvsqb.base2)##
## -1 0 1
## 0 0 2459 0
## 1 0 0 1140
## 2 241 0 0# Make them a factor
td $ dvsqb.cat.b2 <- factor(td $ dvsqb.base2, label = c("Mil", "SQ", "Neg"))
table(td $ dvsqb.cat.b2)##
## Mil SQ Neg
## 241 2459 1140# Mil as the baseline
full.mil <- multinom(dvsqb.cat.b2 ~ slc3b.fac + demdum + milratio + alliance +
strvalue + ethvalue1 + endriv5b + sqtime1,
data = td)## # weights: 30 (18 variable)
## initial value 4218.671188
## iter 10 value 3151.532819
## iter 20 value 2977.439351
## final value 2966.553419
## converged# SQ as the baseline
full.sq <- multinom(dvsqb.cat ~ slc3b.fac + demdum + milratio + alliance +
strvalue + ethvalue1 + endriv5b + sqtime1,
data = td)## # weights: 30 (18 variable)
## initial value 4218.671188
## iter 10 value 2999.001909
## iter 20 value 2969.558159
## final value 2966.553419
## convergedstargazer(full.mil, full.sq, type = "text",
column.labels = c("SQ v Mil", "Neg v Mil", "Neg v SQ", "Mil v SQ"),
covariate.labels = c("Strong legal claims", "Democracy", "Military balance", "Common security ties",
"Strategic territory", "Ethnic ties", "Enduring rivals", "Sqrt(t)"))##
## ============================================================
## Dependent variable:
## ---------------------------------------
## SQ Neg Mil
## SQ v Mil Neg v Mil Neg v SQ Mil v SQ
## (1) (2) (3) (4)
## ------------------------------------------------------------
## Strong legal claims 0.127 0.744* 0.617*** -0.127
## (0.386) (0.386) (0.169) (0.386)
##
## Democracy 0.480*** 0.794*** 0.314*** -0.480***
## (0.182) (0.185) (0.084) (0.182)
##
## Military balance -1.113*** -1.310*** -0.196 1.113***
## (0.262) (0.273) (0.137) (0.262)
##
## Common security ties 0.107 -0.081 -0.189** -0.107
## (0.163) (0.171) (0.086) (0.163)
##
## Strategic territory -0.210 -0.181 0.029 0.210
## (0.158) (0.164) (0.089) (0.158)
##
## Ethnic ties -0.243 0.050 0.293*** 0.243
## (0.150) (0.156) (0.077) (0.150)
##
## Enduring rivals -1.130*** -0.836*** 0.293*** 1.130***
## (0.148) (0.155) (0.089) (0.148)
##
## Sqrt(t) 1.351*** 0.592** -0.760*** -1.351***
## (0.222) (0.230) (0.083) (0.222)
##
## Constant 2.750*** 2.073*** -0.676*** -2.750***
## (0.208) (0.215) (0.096) (0.208)
##
## ------------------------------------------------------------
## Akaike Inf. Crit. 5,969.107 5,969.107 5,969.107 5,969.107
## ============================================================
## Note: *p<0.1; **p<0.05; ***p<0.01