Duration models
- 1. Preparation
- Goal
- Load the data set
- Key variables
- Model 1: Cox Proportional Hazards Model
- Effect Plot: The survival curvel
- 3. Convert this into a BTSCS data set for a logit model
- 4. BTSCS logit models for replacement
- 6. BTSCS logit models for any termination
- 6. Plot the relationship between p-hat and time
- 7. Effect of minority government
1. Preparation
rm(list = ls()) # delete everything in the memory
library(foreign) # for read.dta
library(reshape)
library(ggplot2) # for graphics
library(stargazer) # Regression table
library(effects) # for effect
library(sjPlot)
library(ggeffects) # effect plots
library(foreign)
library(remotes)
# install_github("davidaarmstrong/damisc")
library(DAMisc) # for btscs
library(survival)Goal
We will estimate the effect of interest using two models (Cox model and BTSCS). The point of this exercise is to see how we can use logit models to obtain approximately the same answer we would get from continuous-time duration models.
Load the data set
We will replicate the duration analysis of Chiba et al.’s (2015) work on government survival. We do this by converting the authors’ duration data into a BTSCS data set. The original data set records the duration of cabinets from 17 democracies in Western Europe after the Second World War. Duration is measured in days (how many days elapsed since the formation of a cabinet until its termination due to dissolution or replacement).
The dataset can be loaded here
cms <- read.dta("govdurat.dta")Here is a description of key variables you’d need in order to convert this data set into a BTSCS one:
duration: Duration of cabinet measured in days elapsed since the formation date (
formdate) until the termination date (enddate).unit: unique ID that identifies each cabinet. As there are 432 cabinets in the data set, this variable ranges from 1 to 432.
censor_replace: one of the three variables that measure “failure” events in the data set. This variable takes the value of 1 if a government is terminated as a result of reshuffle (nonelectoral replacement), and 0 if a government is terminated due to election or for technical reasons, in which case the observation is treated as “censored” and we cannot observe the duration of cabinet until reshuffle. (1 = a hazard event occurred, 0 = no hazard event occurred)censor_discelec: one of the three variables that measure “failure” events in the data set. This variable takes the value of 1 if a government is terminated as a result of election, and 0 if a government is terminated due to reshuffle or for technical reasons, in which case the observation is treated as “censored” and we cannot observe the duration of cabinet until election. (1 = a hazard event occurred, 0 = no hazard event occurred)censor_pool: one of the three variables that measure “failure” events in the data set. This variable takes the value of 1 if a government is terminated as a result of an election (dissolution termination) or a re-shuffle (replacement termination). This is coded as 0 if a government is terminated due to technical reasons, in which case the observation is treated as “censored” and we cannot observe the duration of cabinet until reshuffle or until election. In other words, this variable takes the value of 1 when eithercensor_replaceorcensor_discelecis equal to 1.
The codebook for the independent variables:
- Minority government (
minor): coded as 1 if the cabinet is a minority cabinet (i.e., the parties in the government do not control the majority), 0 otherwise. One would expect that a minority cabinet will experience shorter duration (experience greater risk of termination) - Ideological divisions in coalition (
govdiv): numerical variable taking greater values when the parties in the government are ideologically more divided). One would expect that greater values of this variable are associated with shorter duration of government. - Returnability (
prop_prevgovparties): how strongly government parties believe that they will be able to form a new government in which they are included. Ranges between 0 and 1. Greater values will be associated with shorter duration. - Effective number of legislative parties (
enp) - Polarization index (
sysanmax) - Time remaining in CIEP (
logged) (log max govdurat)
Key variables
- Unit: cabinet in parliamentary democracies
- Time (
govdurat) = duration until cabinet ends due to 1) dissolution or election, or 2) duration until the end of observation period - Failed or censored (
censor_pool): If a cabinet has not failed by the end of the observation period, the cabinet is censored
head(cms, 5)## country_name unit formdate enddate govdurat minor govdiv sysanmax
## 1 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 2 Austria 2 1953-04-02 1956-05-14 1138 0 46.0 1.681212
## 3 Austria 3 1956-06-29 1959-05-12 1047 0 62.8 3.498182
## 4 Austria 4 1959-07-16 1961-04-10 634 0 40.0 0.550303
## 5 Austria 5 1961-04-11 1962-11-20 588 0 40.0 0.550303
## max_govdurat enp prop_prevgovparties censor_pooled censor_replace
## 1 1462 2.87 1 1 0
## 2 1447 2.77 1 1 0
## 3 1441 2.46 1 1 0
## 4 1425 2.35 1 1 1
## 5 790 2.35 1 1 0
## censor_discelec log_max_govdurat
## 1 1 7.287560
## 2 1 7.277248
## 3 1 7.273093
## 4 0 7.261927
## 5 1 6.672033Let’s explore the “failure” variables:
Failure event 1: Replacement termination (cabinet reshuffle)
table(cms $ censor_replace) ##
## 0 1
## 201 231231 cases of non-electoral failure events. The rest (201) are treated as censored.
Failure event 2: Election termination (parliament dissolution)
table(cms $ censor_discelec) ##
## 0 1
## 320 112112 cases of electoral failure events. The rest (320) are treated as censored.
Failure event 3: Pooled
table(cms $ censor_pool) ##
## 0 1
## 89 343# table(cms $ censor_replace, cms $ censor_discelec)343 cases of failure events. The rest (89) are treated as censored.
Model 1: Cox Proportional Hazards Model
The dataframe is already formated for a continuous-time duration analysis. We can estimate a Cox model directly from it.
# cox.mod <-coxph(Surv(time_duration, status) ~ covariates )
cox.mod <-coxph(Surv(govdurat, censor_pooled) ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat, data=cms)
summary(cox.mod)## Call:
## coxph(formula = Surv(govdurat, censor_pooled) ~ minor + enp +
## sysanmax + govdiv + prop_prevgovparties + log_max_govdurat,
## data = cms)
##
## n= 432, number of events= 343
##
## coef exp(coef) se(coef) z Pr(>|z|)
## minor 0.677333 1.968620 0.131321 5.158 2.5e-07 ***
## enp 0.040991 1.041843 0.046867 0.875 0.38178
## sysanmax 0.080709 1.084055 0.027028 2.986 0.00283 **
## govdiv 0.006626 1.006648 0.002792 2.373 0.01765 *
## prop_prevgovparties 0.352111 1.422066 0.139710 2.520 0.01173 *
## log_max_govdurat -1.365705 0.255201 0.110042 -12.411 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## minor 1.9686 0.5080 1.5219 2.5465
## enp 1.0418 0.9598 0.9504 1.1421
## sysanmax 1.0841 0.9225 1.0281 1.1430
## govdiv 1.0066 0.9934 1.0012 1.0122
## prop_prevgovparties 1.4221 0.7032 1.0814 1.8700
## log_max_govdurat 0.2552 3.9185 0.2057 0.3166
##
## Concordance= 0.718 (se = 0.014 )
## Likelihood ratio test= 177.7 on 6 df, p=<2e-16
## Wald test = 210.8 on 6 df, p=<2e-16
## Score (logrank) test = 252.7 on 6 df, p=<2e-16The estimated coefficient of the Cox model is the Hazard Rate (+ = greater risk, - = reduced risk). The exp(coef) is the Hazard Ratio (>1 = = greater risk, <1 = reduced risk).
The interpretation: At a given time, a government that is held by a minority is 97% more likely to experience cabinet reshuffle or parliament dissolution than a government that is held by a majority.
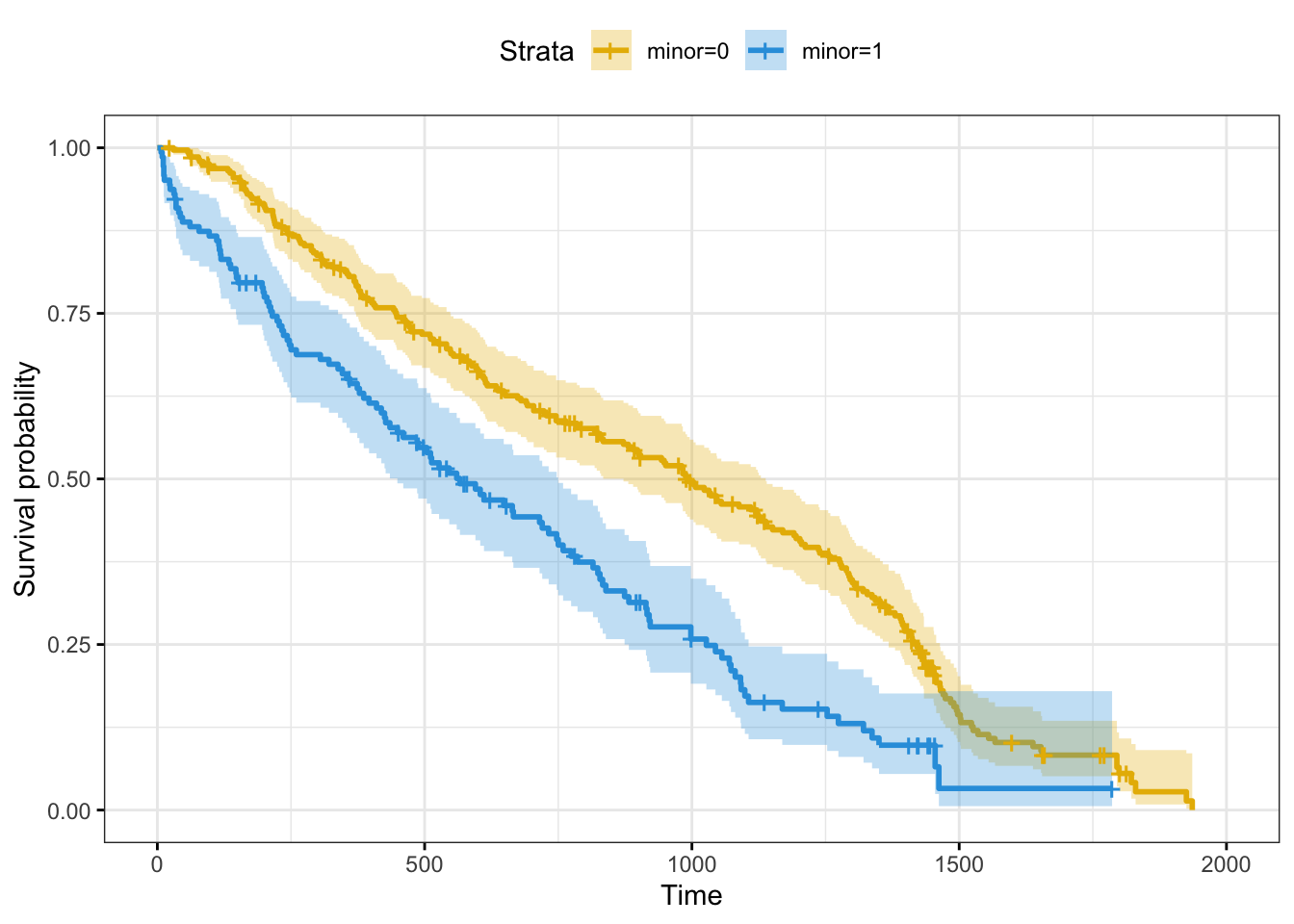
Effect Plot: The survival curvel
Let’s create the effect plot: Create survival curves. We will use the survfit function. The tutorial for this function can be found here.
# https://rpkgs.datanovia.com/survminer/
# install.packages("survminer")
library(survminer)
km_fit <- survfit(Surv(govdurat, censor_pooled) ~ minor , data=cms)
ggsurvplot(
km_fit,
data = cms,
size = 1, # change line size
palette =
c("#E7B800", "#2E9FDF"),# custom color palettes
conf.int = TRUE, # Add confidence interval
# pval = TRUE, # Add p-value
# risk.table = TRUE, # Add risk table
# risk.table.col = "strata",# Risk table color by groups
# legend.labs =
# c("Male", "Female"), # Change legend labels
# risk.table.height = 0.25, # Useful to change when you have multiple groups
ggtheme = theme_bw() # Change ggplot2 theme
)
3. Convert this into a BTSCS data set for a logit model
Step 1: expand using the untable function
expanded <- untable(df = cms, num = cms $ govdurat)
# Make sure this has produced 327799 obs
dim(expanded)## [1] 327799 15Step 2: assign obsID
seq.num <- function(x){
seq(1, max(x))
}
obsID <- tapply(X = expanded $ govdurat,
INDEX = expanded $ unit,
FUN = seq.num)
expanded $ obsID <- unlist(obsID)
head(expanded)## country_name unit formdate enddate govdurat minor govdiv sysanmax
## 1 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 1.1 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 1.2 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 1.3 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 1.4 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## 1.5 Austria 1 1949-11-08 1953-02-25 1205 0 45.8 1.564848
## max_govdurat enp prop_prevgovparties censor_pooled censor_replace
## 1 1462 2.87 1 1 0
## 1.1 1462 2.87 1 1 0
## 1.2 1462 2.87 1 1 0
## 1.3 1462 2.87 1 1 0
## 1.4 1462 2.87 1 1 0
## 1.5 1462 2.87 1 1 0
## censor_discelec log_max_govdurat obsID
## 1 1 7.28756 1
## 1.1 1 7.28756 2
## 1.2 1 7.28756 3
## 1.3 1 7.28756 4
## 1.4 1 7.28756 5
## 1.5 1 7.28756 6Step 3: binary DVs: three types of “failures”
# non-electoral failure (replacement/re-shuffle)
expanded $ binaryDV.rep <- ifelse(expanded $ obsID == expanded $ govdurat &
expanded $ censor_replace == 1, 1, 0)
# electoral failure (dissolution)
expanded $ binaryDV.dis <- ifelse(expanded $ obsID == expanded $ govdurat &
expanded $ censor_discelec == 1, 1, 0)
# two types pooled
expanded $ binaryDV.pool <- ifelse(expanded $ obsID == expanded $ govdurat &
expanded $ censor_pool == 1, 1, 0)Take a look at the distributions of DVs to make sure
# non-electoral
table(cms $ censor_replace) # original continuous-time format##
## 0 1
## 201 231table(expanded $ binaryDV.rep) # BTSCS format##
## 0 1
## 327568 231# electoral
table(cms $ censor_discelec) # original continuous-time format##
## 0 1
## 320 112table(expanded $ binaryDV.dis) # BTSCS format##
## 0 1
## 327687 112# pooled
table(cms $ censor_pool) # original continuous-time format##
## 0 1
## 89 343table(expanded $ binaryDV.pool) # BTSCS format##
## 0 1
## 327456 343Step 4: calender (in this case, calender day)
expanded $ date <- expanded $ formdate + expanded $ obsID - 1Step 5: counter
expanded $ t <- expanded $ obsID - 1Try using BTSCS function to do Step 5 (it doesn’t matter which binary DV you use). It will give you the same result.
expanded.2 <- btscs(expanded, event = "binaryDV.rep", tvar = "date", csunit = "unit")
expanded.3 <- btscs(expanded, event = "binaryDV.dis", tvar = "date", csunit = "unit")
expanded.4 <- btscs(expanded, event = "binaryDV.pool", tvar = "date", csunit = "unit")Let’s compare them with the hand-coded one (should be exactly the same)
table(expanded.2 $ spell == expanded $ t)##
## TRUE
## 327799table(expanded.3 $ spell == expanded $ t)##
## TRUE
## 327799table(expanded.4 $ spell == expanded $ t)##
## TRUE
## 3277994. BTSCS logit models for replacement
# No time component
fit.0.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat, data = expanded, family = binomial(logit))
# Linear, quadratic, and cubic models# Linear time
fit.1.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t, data = expanded, family = binomial(logit))
# Quadratic
fit.2.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2),
data = expanded, family = binomial(logit))
# Cubic
fit.3.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2) + I(t^3),
data = expanded, family = binomial(logit))
# log(t+1)
fit.4.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + log(t+1),
data = expanded, family = binomial(logit))
# sqrt(t)
fit.5.rep <- glm(binaryDV.rep ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + sqrt(t),
data = expanded, family = binomial(logit))
stargazer(fit.0.rep, fit.1.rep, fit.2.rep, fit.3.rep, fit.4.rep, fit.5.rep, type = "text")##
## ======================================================================================
## Dependent variable:
## ------------------------------------------------------------------
## binaryDV.rep
## (1) (2) (3) (4) (5) (6)
## --------------------------------------------------------------------------------------
## minor 0.357** 0.612*** 0.656*** 0.637*** 0.466*** 0.553***
## (0.156) (0.159) (0.161) (0.161) (0.157) (0.158)
##
## enp 0.100* 0.100* 0.101* 0.113** 0.108** 0.103**
## (0.053) (0.052) (0.053) (0.054) (0.053) (0.052)
##
## sysanmax 0.031 0.066* 0.060* 0.052 0.055 0.065*
## (0.035) (0.034) (0.035) (0.035) (0.034) (0.034)
##
## govdiv 0.007** 0.010*** 0.011*** 0.011*** 0.008*** 0.009***
## (0.003) (0.003) (0.003) (0.003) (0.003) (0.003)
##
## prop_prevgovparties 0.323* 0.456*** 0.499*** 0.495*** 0.346** 0.410**
## (0.172) (0.172) (0.175) (0.176) (0.171) (0.171)
##
## log_max_govdurat -0.907*** -1.450*** -1.330*** -1.427*** -1.533*** -1.539***
## (0.110) (0.116) (0.119) (0.126) (0.142) (0.128)
##
## t 0.002*** 0.0002 0.004***
## (0.0002) (0.001) (0.001)
##
## I(t2) 0.00000*** -0.00000***
## (0.00000) (0.00000)
##
## I(t3) 0.000***
## (0.000)
##
## log(t + 1) 0.715***
## (0.098)
##
## sqrt(t) 0.085***
## (0.009)
##
## Constant -1.688** 0.768 0.291 0.452 -1.707** 0.627
## (0.840) (0.798) (0.805) (0.824) (0.848) (0.829)
##
## --------------------------------------------------------------------------------------
## Observations 327,799 327,799 327,799 327,799 327,799 327,799
## Log Likelihood -1,867.485 -1,815.224 -1,809.986 -1,804.443 -1,831.052 -1,820.518
## Akaike Inf. Crit. 3,748.970 3,646.449 3,637.971 3,628.887 3,678.104 3,657.036
## ======================================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01Cubic model is the best
Comparing the results with those from Table 3 on page 54 (first column), the signs are different. This is because the BTSCS results show the effects of independent variables on the risk (probability) of government failure, whereas those reported in Table 3 show the effect of variables on duration.
5. BTSCS logit models for duration until electoral termination
# No time component
fit.0.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat, data = expanded, family = binomial(logit))
# Linear time
fit.1.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t, data = expanded, family = binomial(logit))
# Quadratic
fit.2.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2),
data = expanded, family = binomial(logit))
# Cubic
fit.3.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2) + I(t^3),
data = expanded, family = binomial(logit))
# log(t+1)
fit.4.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + log(t+1),
data = expanded, family = binomial(logit))
# sqrt(t)
fit.5.dis <- glm(binaryDV.dis ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + sqrt(t),
data = expanded, family = binomial(logit))
stargazer(fit.0.dis, fit.1.dis, fit.2.dis, fit.3.dis, fit.4.dis, fit.5.dis, type = "text")##
## ===============================================================================
## Dependent variable:
## -----------------------------------------------------------
## binaryDV.dis
## (1) (2) (3) (4) (5) (6)
## -------------------------------------------------------------------------------
## minor 0.488** 0.713*** 0.711*** 0.721*** 0.590*** 0.667***
## (0.221) (0.223) (0.224) (0.224) (0.222) (0.222)
##
## enp -0.127 -0.121 -0.121 -0.120 -0.120 -0.119
## (0.094) (0.093) (0.093) (0.092) (0.095) (0.094)
##
## sysanmax 0.090** 0.117*** 0.117*** 0.121*** 0.108** 0.116***
## (0.045) (0.045) (0.045) (0.045) (0.044) (0.044)
##
## govdiv -0.006 -0.004 -0.004 -0.004 -0.006 -0.005
## (0.006) (0.006) (0.006) (0.006) (0.006) (0.006)
##
## prop_prevgovparties 0.001 0.105 0.104 0.101 0.025 0.071
## (0.228) (0.230) (0.230) (0.229) (0.228) (0.229)
##
## log_max_govdurat -0.697*** -1.247*** -1.252*** -1.175*** -1.222*** -1.318***
## (0.186) (0.189) (0.197) (0.195) (0.222) (0.207)
##
## t 0.002*** 0.002** -0.001
## (0.0002) (0.001) (0.002)
##
## I(t2) -0.00000 0.00000*
## (0.00000) (0.00000)
##
## I(t3) -0.000*
## (0.000)
##
## log(t + 1) 0.628***
## (0.134)
##
## sqrt(t) 0.082***
## (0.013)
##
## Constant -2.704* -0.115 -0.098 -0.204 -2.882** -0.383
## (1.420) (1.342) (1.356) (1.327) (1.444) (1.396)
##
## -------------------------------------------------------------------------------
## Observations 327,799 327,799 327,799 327,799 327,799 327,799
## Log Likelihood -992.961 -968.463 -968.459 -966.518 -978.442 -970.870
## Akaike Inf. Crit. 1,999.921 1,952.925 1,954.917 1,953.035 1,972.884 1,957.739
## ===============================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01Linear time model is the best
6. BTSCS logit models for any termination
# No time component
fit.0.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat, data = expanded, family = binomial(logit))
# Linear time
fit.1.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t, data = expanded, family = binomial(logit))
# Quadratic
fit.2.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2),
data = expanded, family = binomial(logit))
# Cubic
fit.3.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2) + I(t^3),
data = expanded, family = binomial(logit))
# log(t+1)
fit.4.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + log(t+1),
data = expanded, family = binomial(logit))
# sqrt(t)
fit.5.pool <- glm(binaryDV.pool ~ minor + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + sqrt(t),
data = expanded, family = binomial(logit))
# stargazer(fit.0.pool, fit.1.pool, fit.2.pool, fit.3.pool, fit.4.pool, fit.5.pool, type = "text")Cubic is the best.
You will see that we can use logit models to obtain approximately the same answer we would get from continuous-time duration models. The estimated coef is similarly around 0.5-0.6 in terms of the Hazard Ratio.
6. Plot the relationship between p-hat and time
This may take a while.
plot(effect(term = "t", mod = fit.3.pool), type = "response", rug = FALSE)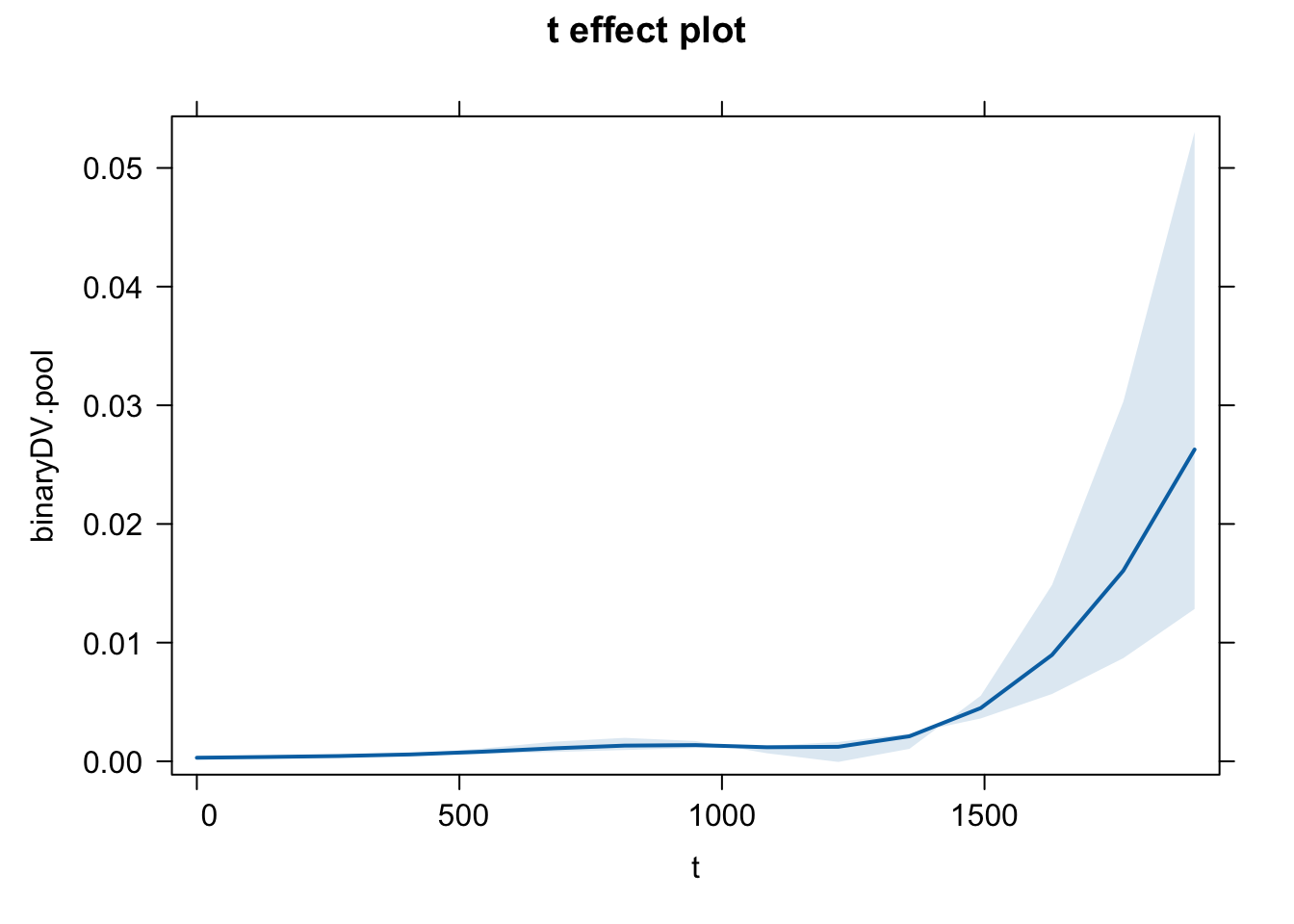
# The risk of termination is mildly increasing over time. The rate of increase
# gets bigger especially after about 1000 days. 7. Effect of minority government
eff.minor <- effect(term = "minor",
mod = fit.3.pool, typical = median,
given.values = c("t" = 1095, "I(t^2)" = 1095^2, "I(t^3)" = 1095^3))
eff.minor##
## minor effect
## minor
## 0 0.2 0.5 0.8 1
## 0.001353140 0.001544572 0.001883578 0.002296818 0.002621404# 0.002621404 -0.001353140
fit.3.pool <- glm(binaryDV.pool ~ factor(minor) + enp + sysanmax + govdiv + prop_prevgovparties +
log_max_govdurat + t + I(t^2) + I(t^3),
data = expanded, family = binomial(logit))
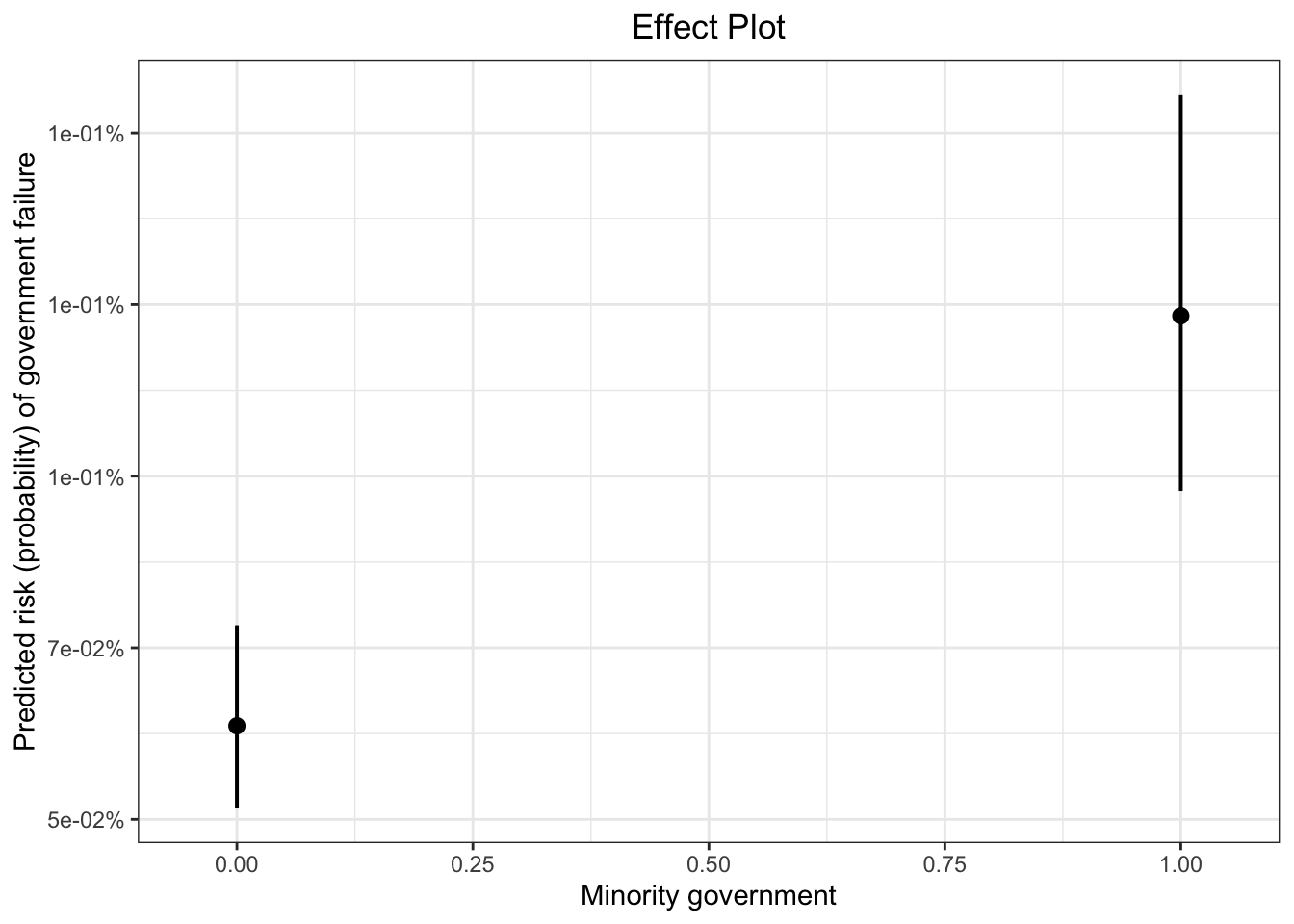
plot_model(fit.3.pool, type = "pred", terms = c("minor"), ci.lvl = 0.95, bpe.style = "line", robust = T, legend.title = "", vcov.type = c("HC3"), colors="bw") +
theme_bw() +
ggtitle(element_blank()) +
xlab("Minority government") + ylab("Predicted risk (probability) of government failure") +
labs(title = "Effect Plot") +
theme(plot.title = element_text(hjust = 0.5)) 