Count models
- 1. Preparation
- 2. load the data set
- 3. Take a look at the data set and figure out the unit
- 4. Distribution of the DV
- 5-6. Independent variable
- 7. Estimate a Poisson model
- Quasipoisson
- 8-9. Estimate a Negative Binomial Model
- 10. effect of discriminated minority
- 11. effect of executive constraint
- 12. effect of GINI
- 13. Quadratic model
- 14. effect of GINI based on model (a)
- 15. effect of GINI based on model (b)
- Zero-inflated NegBin
- Descriptive Stats: bar chart
- Descriptive Stats: map
1. Preparation
rm(list = ls()) # delete everything in the memory
library(foreign) # for read.dta
library(ggplot2) # for graphics
library(stargazer) # Regression table
library(effects) # for effect
library(rworldmap) # for drawing maps
library(countrycode) # for countrycode
library(MASS) # necessary for glm.nb
library(sjPlot)
library(pscl) # zeroinf model
library(ggeffects) # effect plots3. Take a look at the data set and figure out the unit
head(att)## Country COW Year Durable Executive GINI logpop logarea Partic laglogGNI
## 1 United S 2 1970 161 5.7 34.1 5.323254 16.03057 3.0 NA
## 2 United S 2 1971 162 5.7 34.3 5.335902 16.03057 3.0 8.516061
## 3 United S 2 1972 163 5.7 34.5 5.346631 16.03057 3.0 8.583423
## 4 United S 2 1973 164 5.7 34.4 5.356162 16.03057 2.5 8.671758
## 5 United S 2 1974 165 5.7 34.2 5.365275 16.03057 2.5 8.776861
## 6 United S 2 1975 166 5.7 34.4 5.375140 16.03057 2.5 8.849730
## lagHDI GTDDomestic lagECDIS23or4 lagECDIS0 lagECDIS1 lagNoMAR
## 1 NA 49 NA NA NA NA
## 2 0.866 90 1 0 0 0
## 3 0.866 16 1 0 0 0
## 4 0.866 33 1 0 0 0
## 5 0.866 24 1 0 0 0
## 6 0.866 94 1 0 0 0
## lagMARbutNoECDIS
## 1 NA
## 2 0
## 3 0
## 4 0
## 5 0
## 6 0## Figure out the data structure
### Country
# List of countries
unique(att $ Country)## [1] "United S" "Canada" "Cuba" "Haiti" "Dominica" "Jamaica"
## [7] "Trinidad" "Barbados" "Grenada" "Mexico" "Belize" "Guatemal"
## [13] "Honduras" "ElSalvad" "Nicaragu" "Costa Ri" "Panama" "Colombia"
## [19] "Venezuel" "Guyana" "Suriname" "Ecuador" "Peru" "Brazil"
## [25] "Bolivia" "Paraguay" "Chile" "Argentin" "Uruguay" "UnitedKi"
## [31] "Ireland" "Netherla" "Belgium" "Luxembou" "France" "Switzerl"
## [37] "Spain" "Portugal" "Germany" "Poland" "Austria" "Hungary"
## [43] "CzechRep" "Slovakia" "Italy" "Malta" "Albania" "Yugoslav"
## [49] "Croatia" "Bosnia" "Slovenia" "Macedoni" "Greece" "Cyprus"
## [55] "Bulgaria" "Romania" "Lithuani" "Moldova" "Estonia" "Latvia"
## [61] "Russia" "Azerbaij" "Armenia" "Ukraine" "Tajiksta" "Georgia"
## [67] "Uzbekist" "Kazakhst" "Finland" "Sweden" "Norway" "Denmark"
## [73] "Iceland" "Cape Ver" "SaoTomeP" "GuineaBi" "Gambia" "Mali"
## [79] "Senegal" "Benin" "Mauritan" "Niger" "Coted'Iv" "Guinea"
## [85] "BurkinaF" "Equatori" "Liberia" "SierraLe" "Ghana" "Togo"
## [91] "Cameroon" "Nigeria" "Gabon" "CentralA" "Chad" "CongoBra"
## [97] "CongoKin" "Uganda" "Kenya" "Tanzania" "Burundi" "Rwanda"
## [103] "Somalia" "Djibouti" "Ethiopia" "Eritrea" "Angola" "Mozambiq"
## [109] "Zambia" "Zimbabwe" "Malawi" "SouthAfr" "Namibia" "Lesotho"
## [115] "Botswana" "Swazilan" "Madagasc" "Comoros" "Mauritiu" "Seychell"
## [121] "Morocco" "Algeria" "Tunisia" "Libya" "Sudan" "Iran"
## [127] "Turkey" "Iraq" "Egypt" "Syria" "Lebanon" "Jordan"
## [133] "Israel" "SaudiAra" "Yemen" "Kuwait" "Bahrain" "Qatar"
## [139] "Oman" "UnitedAr" "Afghanis" "Turkmeni" "Kyrgyz" "China"
## [145] "Mongolia" "Taiwan" "NorthKor" "SouthKor" "Japan" "India"
## [151] "Bhutan" "Banglade" "Pakistan" "Burma" "SriLanka" "Maldives"
## [157] "Nepal" "Thailand" "Cambodia" "Laos" "Vietnam" "Malaysia"
## [163] "Singapor" "Brunei" "Philippi" "Indonesi" "East Tim" "Australi"
## [169] "PapuaNew" "NewZeala" "SolomonI" "Fiji"# Number of countries
length(unique(att $ Country))## [1] 172# Distribution
table(att $ Country)##
## Afghanis Albania Algeria Angola Argentin Armenia Australi Austria
## 37 37 37 37 37 37 37 37
## Azerbaij Bahrain Banglade Barbados Belgium Belize Benin Bhutan
## 37 37 37 37 37 37 37 37
## Bolivia Bosnia Botswana Brazil Brunei Bulgaria BurkinaF Burma
## 37 37 37 37 37 37 37 37
## Burundi Cambodia Cameroon Canada Cape Ver CentralA Chad Chile
## 37 37 37 37 37 37 37 37
## China Colombia Comoros CongoBra CongoKin Costa Ri Coted'Iv Croatia
## 37 37 37 37 37 37 37 37
## Cuba Cyprus CzechRep Denmark Djibouti Dominica East Tim Ecuador
## 37 37 37 37 37 37 37 37
## Egypt ElSalvad Equatori Eritrea Estonia Ethiopia Fiji Finland
## 37 37 37 37 37 37 37 37
## France Gabon Gambia Georgia Germany Ghana Greece Grenada
## 37 37 37 37 37 37 37 37
## Guatemal Guinea GuineaBi Guyana Haiti Honduras Hungary Iceland
## 37 37 37 37 37 37 37 37
## India Indonesi Iran Iraq Ireland Israel Italy Jamaica
## 37 37 37 37 37 37 37 37
## Japan Jordan Kazakhst Kenya Kuwait Kyrgyz Laos Latvia
## 37 37 37 37 37 37 37 37
## Lebanon Lesotho Liberia Libya Lithuani Luxembou Macedoni Madagasc
## 37 37 37 37 37 37 37 37
## Malawi Malaysia Maldives Mali Malta Mauritan Mauritiu Mexico
## 37 37 37 37 37 37 37 37
## Moldova Mongolia Morocco Mozambiq Namibia Nepal Netherla NewZeala
## 37 37 37 37 37 37 37 37
## Nicaragu Niger Nigeria NorthKor Norway Oman Pakistan Panama
## 37 37 37 37 37 37 37 37
## PapuaNew Paraguay Peru Philippi Poland Portugal Qatar Romania
## 37 37 37 37 37 37 37 37
## Russia Rwanda SaoTomeP SaudiAra Senegal Seychell SierraLe Singapor
## 37 37 37 37 37 37 37 37
## Slovakia Slovenia SolomonI Somalia SouthAfr SouthKor Spain SriLanka
## 37 37 37 37 37 37 37 37
## Sudan Suriname Swazilan Sweden Switzerl Syria Taiwan Tajiksta
## 37 37 37 37 37 37 37 37
## Tanzania Thailand Togo Trinidad Tunisia Turkey Turkmeni Uganda
## 37 37 37 37 37 37 37 37
## Ukraine United S UnitedAr UnitedKi Uruguay Uzbekist Venezuel Vietnam
## 37 37 37 37 37 37 37 37
## Yemen Yugoslav Zambia Zimbabwe
## 37 37 37 37# Each country has 37 observations (37 years)
### Year
# Range of years
range(att $ Year)## [1] 1970 2006# Number of years
length(unique(att $ Year))## [1] 37# Distribution
table(att $ Year)##
## 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1984 1985
## 172 172 172 172 172 172 172 172 172 172 172 172 172 172 172 172
## 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001
## 172 172 172 172 172 172 172 172 172 172 172 172 172 172 172 172
## 2002 2003 2004 2005 2006
## 172 172 172 172 172# Each year has 172 observations (172 countries)4. Distribution of the DV
# Numerical summary
summary(att $ GTDDomestic)## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.000 0.000 0.000 7.491 1.000 524.000 471# Graphical summary (overall)
g <- ggplot(data = att, aes(x = GTDDomestic)) + geom_histogram()
g <- g + theme(axis.text.x = element_text(size = 12))
g <- g + xlab("Number of Domestic Terrorist Attacks") + ylab("Number of Country-years")
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.## Warning: Removed 471 rows containing non-finite outside the scale range
## (`stat_bin()`).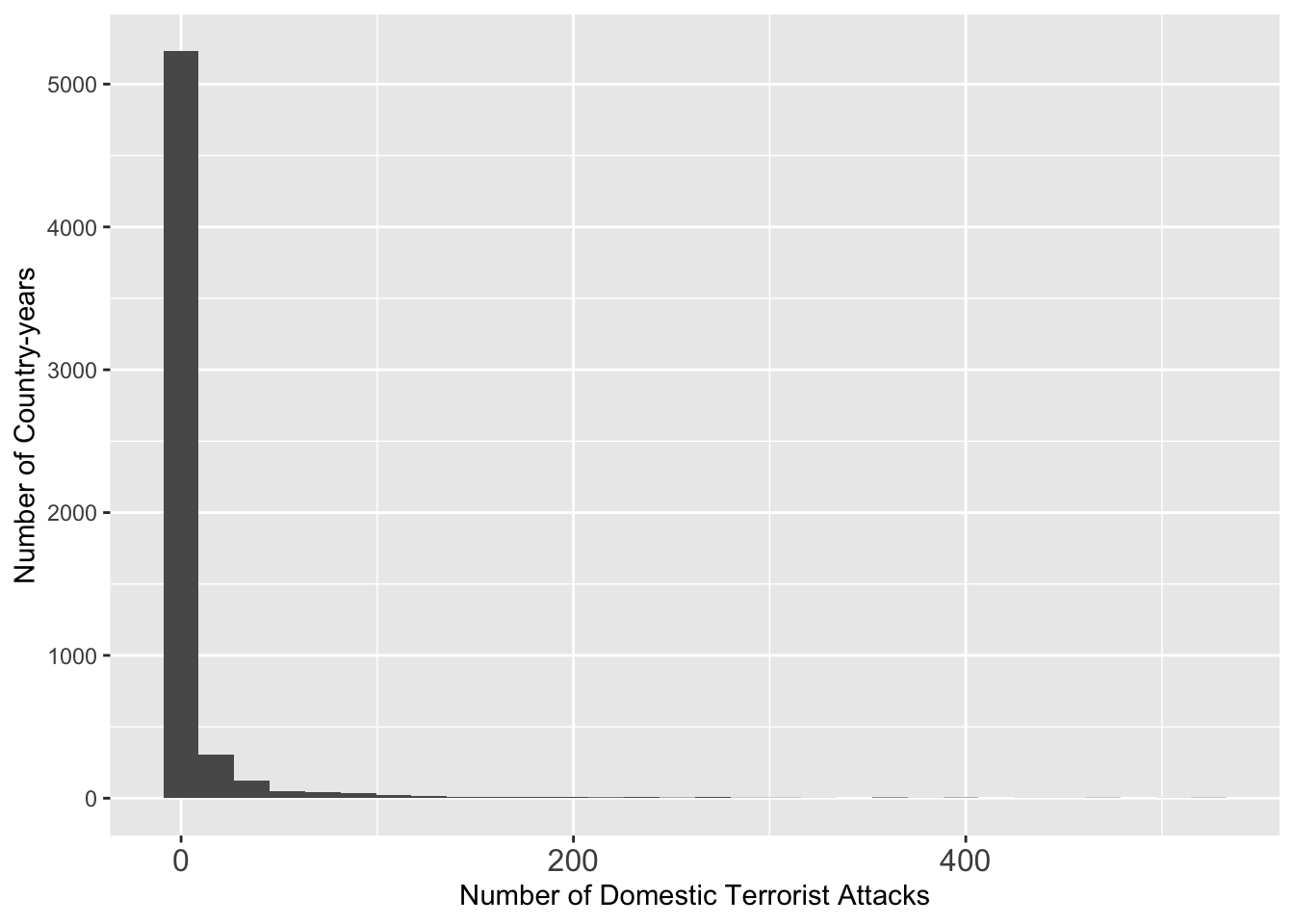
# ggsave(file = "dv_overall.pdf", width = 8, height = 4)Let’s graph by year
## 2005
g <- ggplot(data = att[att $ Year == 2005, ], aes(x = GTDDomestic)) + geom_histogram()
g <- g + theme(axis.text.x = element_text(size = 12))
g <- g + xlab("Number of Domestic Terrorist Attacks, 2005") + ylab("Number of Country-years")
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.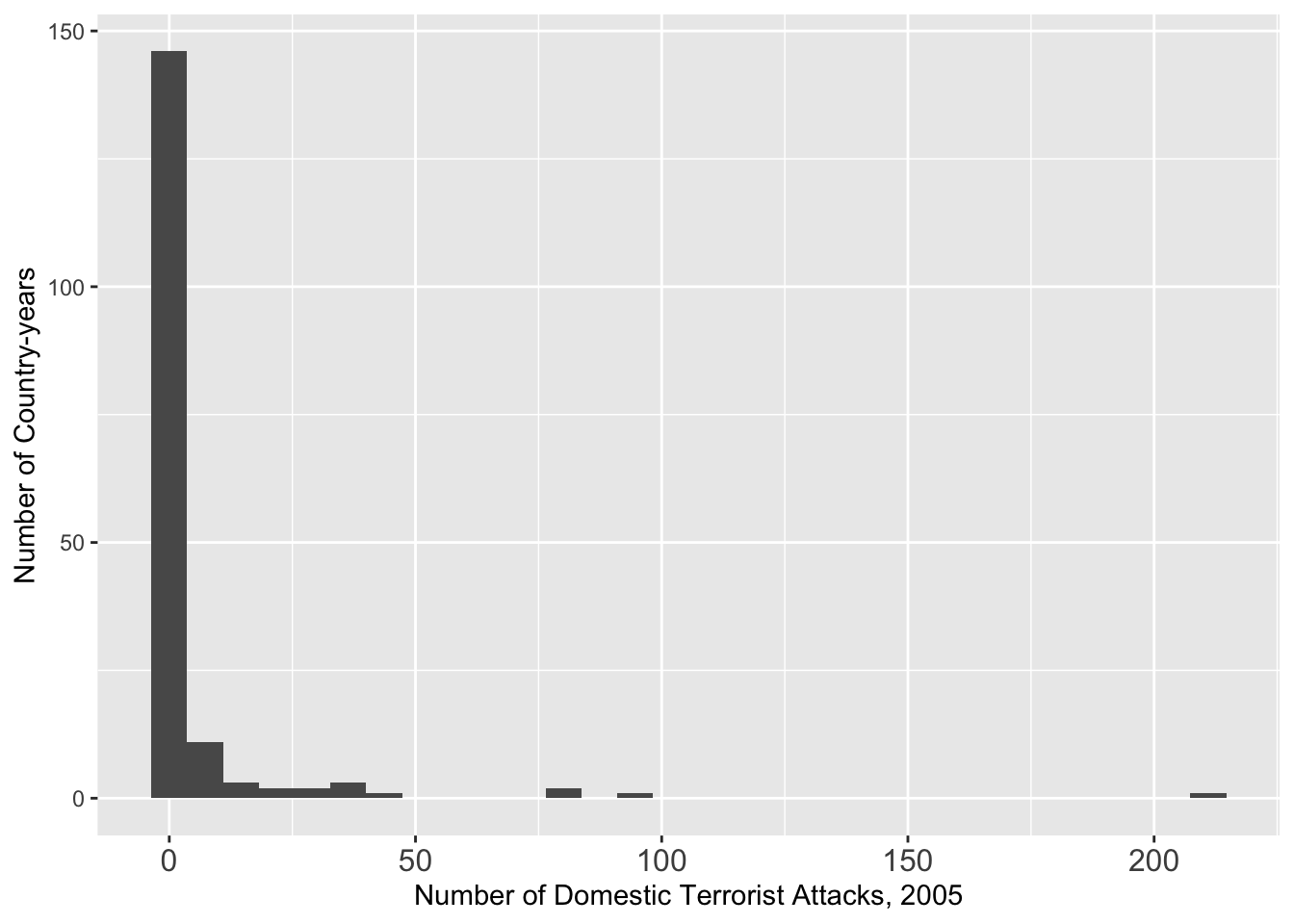
# ggsave(file = "dv_2005.pdf", width = 8, height = 4)
## 1995
g <- ggplot(data = att[att $ Year == 1995, ], aes(x = GTDDomestic)) + geom_histogram()
g <- g + theme(axis.text.x = element_text(size = 12))
g <- g + xlab("Number of Domestic Terrorist Attacks, 1995") + ylab("Number of Country-years")
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.## Warning: Removed 1 row containing non-finite outside the scale range
## (`stat_bin()`).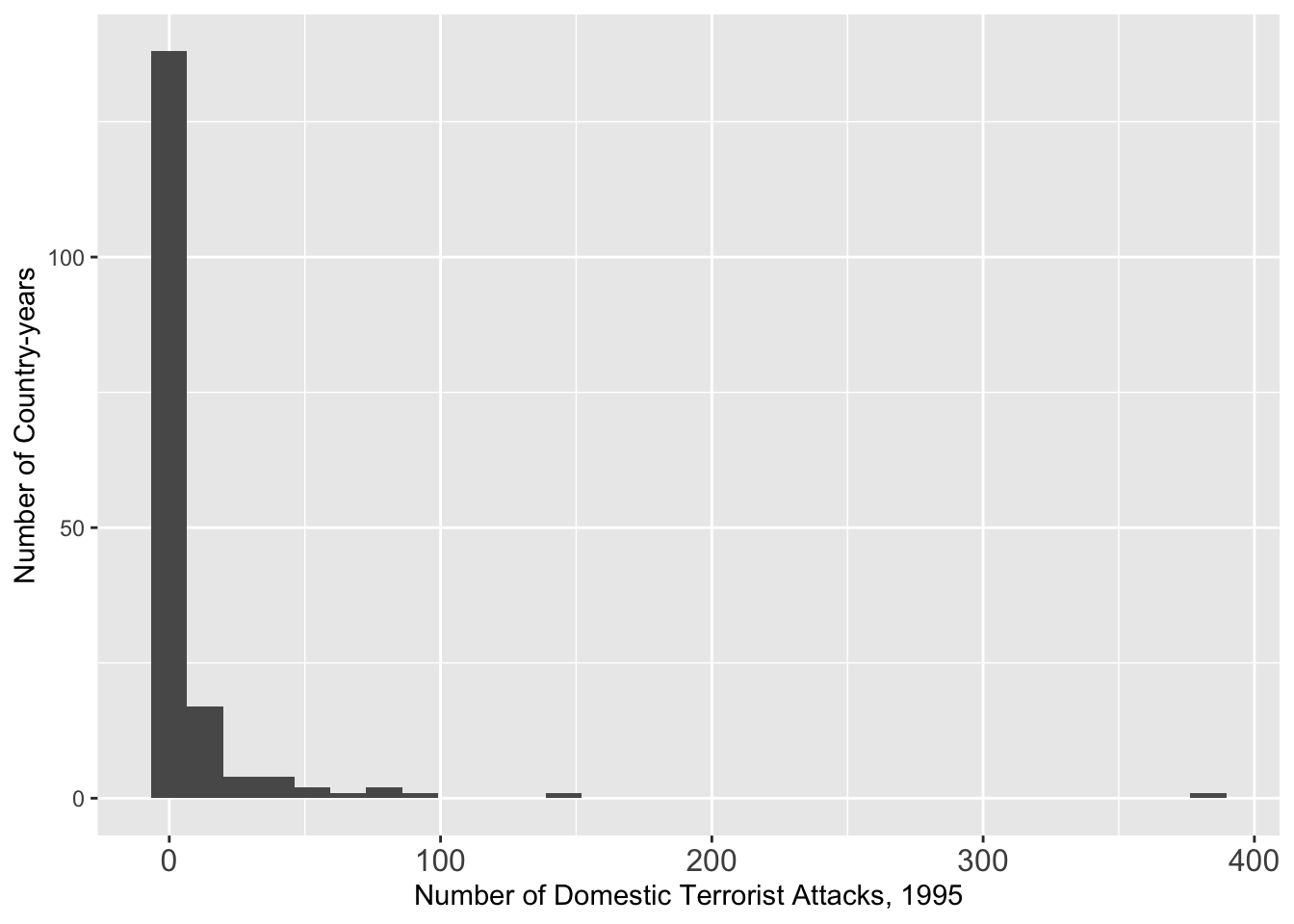
# ggsave(file = "dv_1995.pdf", width = 8, height = 4)We see a long tailed distribution
We can also do all years together by using facet_wrap
## One graph per year
g <- ggplot(data = att, aes(x = GTDDomestic)) + geom_histogram()
g <- g + theme(axis.text.x = element_text(size = 10))
g <- g + facet_wrap( ~ Year, ncol = 8)
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.## Warning: Removed 471 rows containing non-finite outside the scale range
## (`stat_bin()`).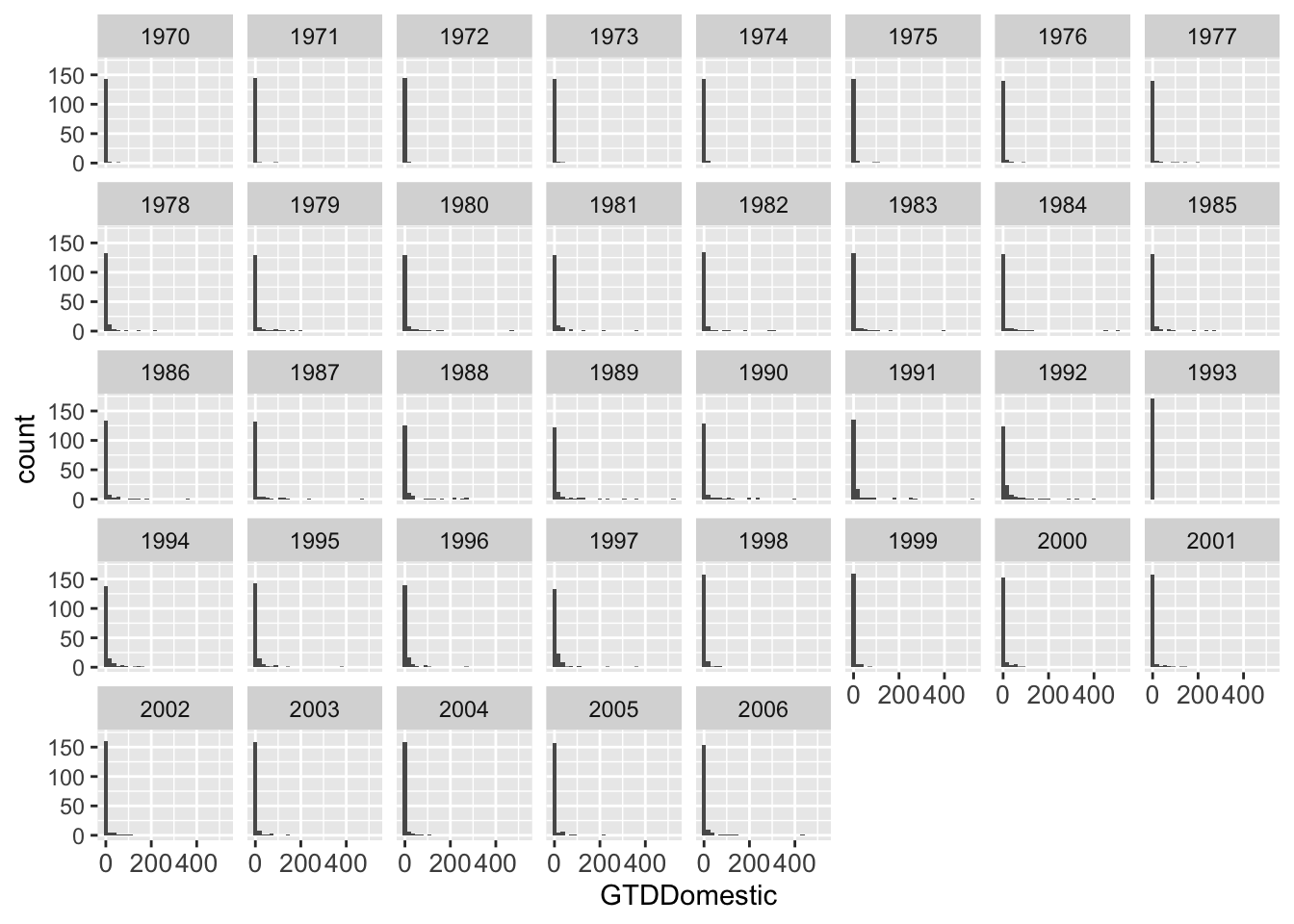
# ggsave(file = "dv_byyear.pdf", width = 8, height = 4)Or, we can do one graph per country
## selected countries
g <- ggplot(data = att[att $ Country=="Algeria" | att $ Country == "Chile" | att $ Country == "Colombia" |
att $ Country == "India" | att $ Country == "Spain" | att $ Country == "Israel" |
att $ Country == "UnitedKi" | att $ Country == "Peru" | att $ Country == "Russia", ],
aes(x = GTDDomestic)) + geom_histogram()
g <- g + facet_wrap( ~ Country, ncol = 3)
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.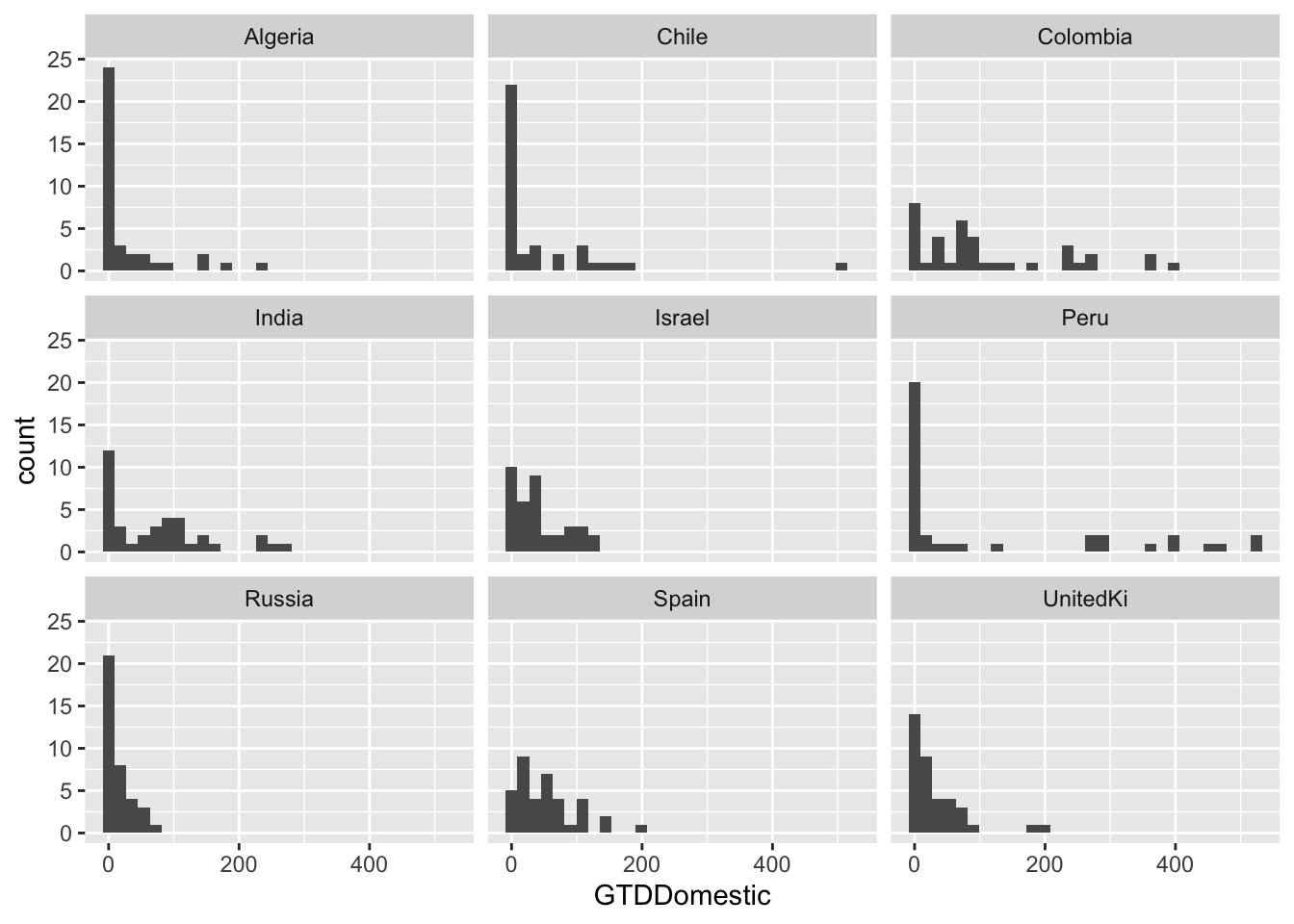
# ggsave(file = "dv_selcnt.pdf", width = 8, height = 6)5-6. Independent variable
# The main IV: presence of economically discriminated minority groups
table(att $ lagECDIS23or4)##
## 0 1
## 1592 1546# recode it
att $ lagECDIS23or4 <- factor(att $ lagECDIS23or4, labels = c("No", "Yes"))
# distribution
table(att $ lagECDIS23or4)##
## No Yes
## 1592 1546# Brief codebook
# GTDDomestic "Count of Domestic Terrorist Attack"
# lagECDIS23or4 "Economic Discrimination"
# laglogGNI "GNI per capita" GNI (= Gross National Income) is kind of like GDP
# GINI "GINI coefficient" GINI coeff is a measure of inequality
# logpop "Log Population"
# logarea "Log Area"
# Durable "Regime Age" How long has the regime lasted?
# Partic "Political Participation" from the Polity IV data set
# Executive "Executive Constraints" from Polity IV data set7. Estimate a Poisson model
fit.pois <- glm(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
laglogGNI + GINI + Partic + Executive ,
data = att,
family = poisson)
summary(fit.pois)##
## Call:
## glm(formula = GTDDomestic ~ lagECDIS23or4 + logpop + logarea +
## Durable + laglogGNI + GINI + Partic + Executive, family = poisson,
## data = att)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.2880623 0.0773047 16.66 <2e-16 ***
## lagECDIS23or4Yes 1.2166122 0.0196578 61.89 <2e-16 ***
## logpop 0.7040018 0.0070424 99.97 <2e-16 ***
## logarea -0.3182635 0.0059027 -53.92 <2e-16 ***
## Durable -0.0030981 0.0002351 -13.18 <2e-16 ***
## laglogGNI 0.2088400 0.0056633 36.88 <2e-16 ***
## GINI 0.0384529 0.0008905 43.18 <2e-16 ***
## Partic -0.2219955 0.0078571 -28.25 <2e-16 ***
## Executive -0.1376723 0.0042362 -32.50 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 103889 on 2963 degrees of freedom
## Residual deviance: 75743 on 2955 degrees of freedom
## (3400 observations deleted due to missingness)
## AIC: 79990
##
## Number of Fisher Scoring iterations: 7See that “Dispersion parameter for poisson family taken to be 1”
Let’s do an over-dispersion test:
library(AER)
dispersiontest(fit.pois,trafo=1)##
## Overdispersion test
##
## data: fit.pois
## z = 5.194, p-value = 1.029e-07
## alternative hypothesis: true alpha is greater than 0
## sample estimates:
## alpha
## 66.79289Here we clearly see that there is evidence of overdispersion (c is estimated to be 66.79) which speaks quite strongly against the assumption of equidispersion (i.e. c=0). It means that you should probably use an quasipoission or Neg-Bin model
Quasipoisson
fit.qpois <- glm(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
laglogGNI + GINI + Partic + Executive ,
data = att,
family = quasipoisson)
summary(fit.qpois)##
## Call:
## glm(formula = GTDDomestic ~ lagECDIS23or4 + logpop + logarea +
## Durable + laglogGNI + GINI + Partic + Executive, family = quasipoisson,
## data = att)
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.288062 0.636397 2.024 0.043061 *
## lagECDIS23or4Yes 1.216612 0.161830 7.518 7.34e-14 ***
## logpop 0.704002 0.057975 12.143 < 2e-16 ***
## logarea -0.318264 0.048593 -6.550 6.78e-11 ***
## Durable -0.003098 0.001935 -1.601 0.109473
## laglogGNI 0.208840 0.046622 4.479 7.77e-06 ***
## GINI 0.038453 0.007331 5.245 1.67e-07 ***
## Partic -0.221996 0.064682 -3.432 0.000607 ***
## Executive -0.137672 0.034873 -3.948 8.07e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 67.77105)
##
## Null deviance: 103889 on 2963 degrees of freedom
## Residual deviance: 75743 on 2955 degrees of freedom
## (3400 observations deleted due to missingness)
## AIC: NA
##
## Number of Fisher Scoring iterations: 7You see that the point est. doesn’t change. And the dispersion parameter for quasipoisson family taken to be 67.77105
8-9. Estimate a Negative Binomial Model
fit.nb <- glm.nb(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
laglogGNI + GINI + Partic + Executive ,
data = att)
summary(fit.nb)##
## Call:
## glm.nb(formula = GTDDomestic ~ lagECDIS23or4 + logpop + logarea +
## Durable + laglogGNI + GINI + Partic + Executive, data = att,
## init.theta = 0.1854585565, link = log)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.275721 0.555304 0.497 0.62
## lagECDIS23or4Yes 1.457271 0.101898 14.301 < 2e-16 ***
## logpop 1.081761 0.046340 23.344 < 2e-16 ***
## logarea -0.347607 0.035649 -9.751 < 2e-16 ***
## Durable -0.008524 0.001859 -4.586 4.53e-06 ***
## laglogGNI 0.215428 0.039540 5.448 5.08e-08 ***
## GINI 0.049304 0.005873 8.395 < 2e-16 ***
## Partic -0.298552 0.048652 -6.137 8.43e-10 ***
## Executive -0.158715 0.032229 -4.925 8.45e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for Negative Binomial(0.1855) family taken to be 1)
##
## Null deviance: 3348.0 on 2963 degrees of freedom
## Residual deviance: 2238.8 on 2955 degrees of freedom
## (3400 observations deleted due to missingness)
## AIC: 11270
##
## Number of Fisher Scoring iterations: 1
##
##
## Theta: 0.18546
## Std. Err.: 0.00683
##
## 2 x log-likelihood: -11250.44200stargazer(fit.pois, fit.nb, type = "text")##
## ==============================================
## Dependent variable:
## ----------------------------
## GTDDomestic
## Poisson negative
## binomial
## (1) (2)
## ----------------------------------------------
## lagECDIS23or4Yes 1.217*** 1.457***
## (0.020) (0.102)
##
## logpop 0.704*** 1.082***
## (0.007) (0.046)
##
## logarea -0.318*** -0.348***
## (0.006) (0.036)
##
## Durable -0.003*** -0.009***
## (0.0002) (0.002)
##
## laglogGNI 0.209*** 0.215***
## (0.006) (0.040)
##
## GINI 0.038*** 0.049***
## (0.001) (0.006)
##
## Partic -0.222*** -0.299***
## (0.008) (0.049)
##
## Executive -0.138*** -0.159***
## (0.004) (0.032)
##
## Constant 1.288*** 0.276
## (0.077) (0.555)
##
## ----------------------------------------------
## Observations 2,964 2,964
## Log Likelihood -39,985.850 -5,626.221
## theta 0.185*** (0.007)
## Akaike Inf. Crit. 79,989.700 11,270.440
## ==============================================
## Note: *p<0.1; **p<0.05; ***p<0.01Since theta != 0 (significantly different from zero), we should prefer the Negative Binomial model to the Poisson model.
10. effect of discriminated minority
eff.mar <- effect(term = "lagECDIS23or4", mod = fit.nb)
eff.mar##
## lagECDIS23or4 effect
## lagECDIS23or4
## No Yes
## 1.322761 5.680233# pdf(file = "eff_mar.pdf", width = 10, height = 7)
plot(eff.mar, type = "response",
main = "Effect of Economic Discrimination",
ylab = "Predicted Number of Terrorist Attacks",
xlab = "Economically Discriminated Minority Present?")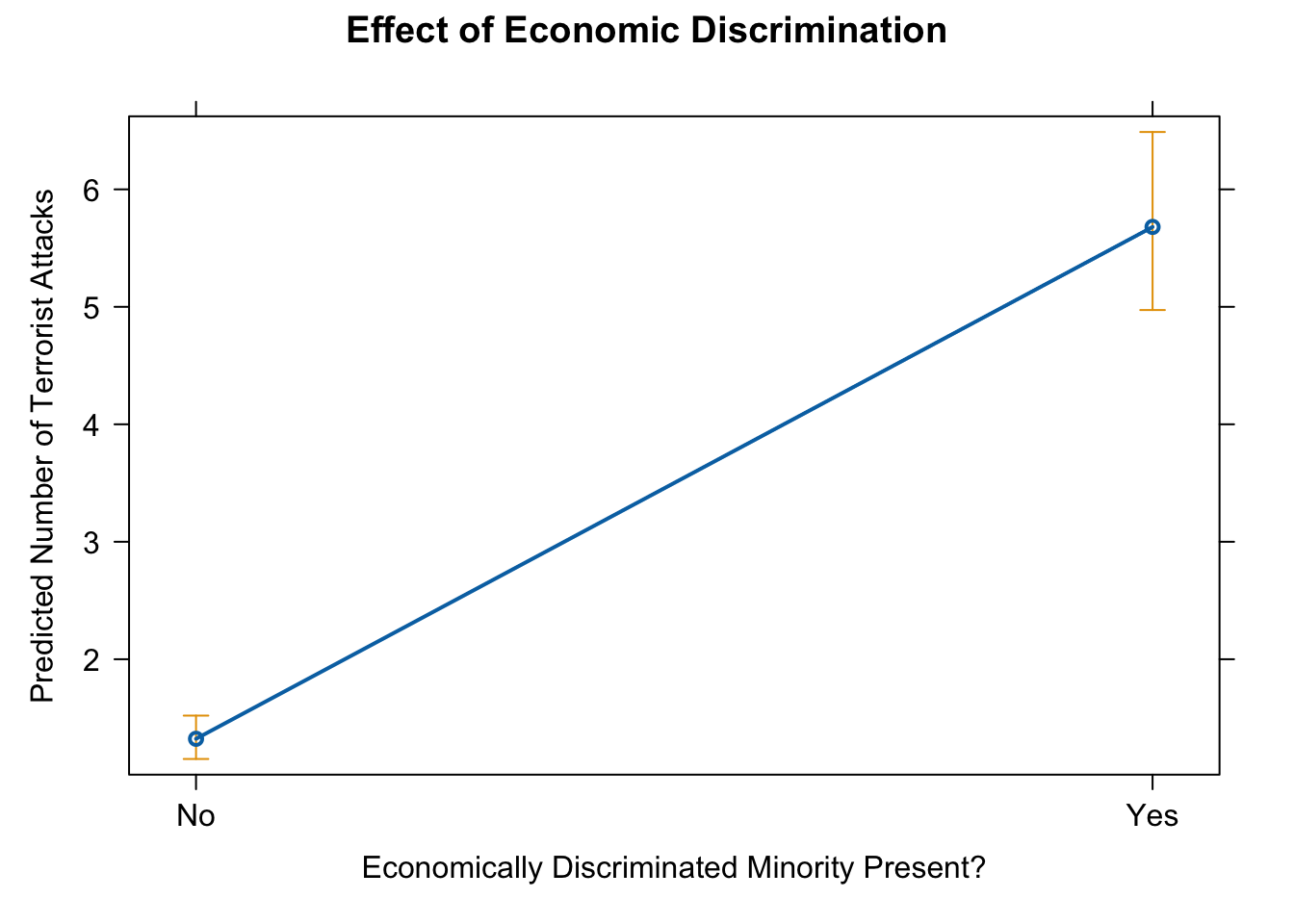
# dev.off()Let’s use ggplot to produce the result.
plot_model(fit.nb, type = "pred", terms = c("lagECDIS23or4"), ci.lvl = 0.95, bpe.style = "line", robust = T, legend.title = "", vcov.type = c("HC3"), colors="bw") +
theme_bw() +
ggtitle(element_blank()) +
xlab("Economic Discrimination") + ylab("Predicted Number of Terrorist Attacks") +
labs(title = "Effect Plot") +
theme(plot.title = element_text(hjust = 0.5)) 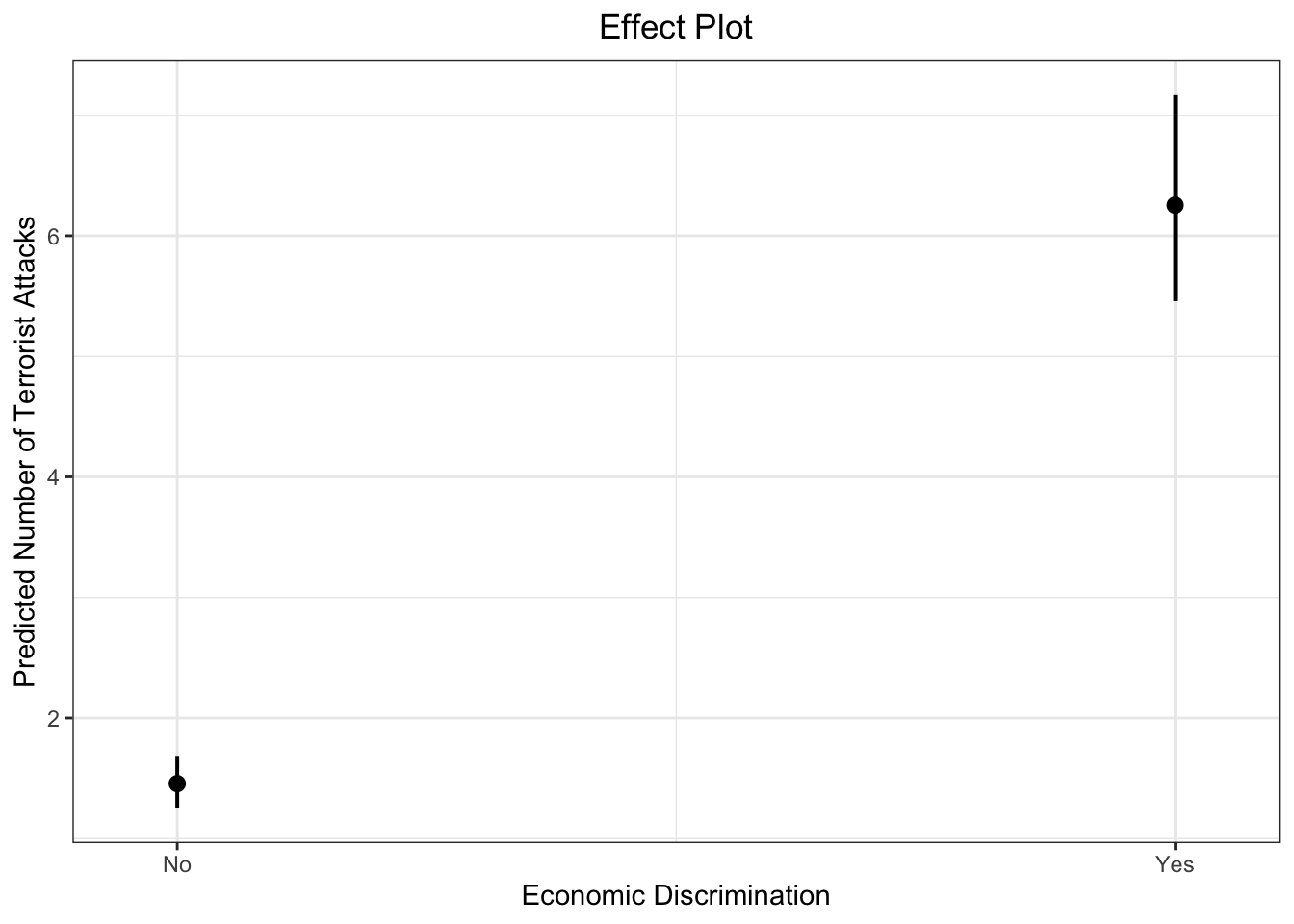
11. effect of executive constraint
eff.exe <- effect(term = "Executive", mod = fit.nb)
eff.exe##
## Executive effect
## Executive
## -8 -4 -1 2 6
## 17.094821 9.060410 5.628081 3.496011 1.852918# pdf(file = "eff_exec.pdf", width = 10, height = 7)
plot(eff.exe, type = "response",
main = "Effect of Executive Constraint",
ylab = "Predicted Number of Terrorist Attacks",
xlab = "Executive Constraint (Polity)")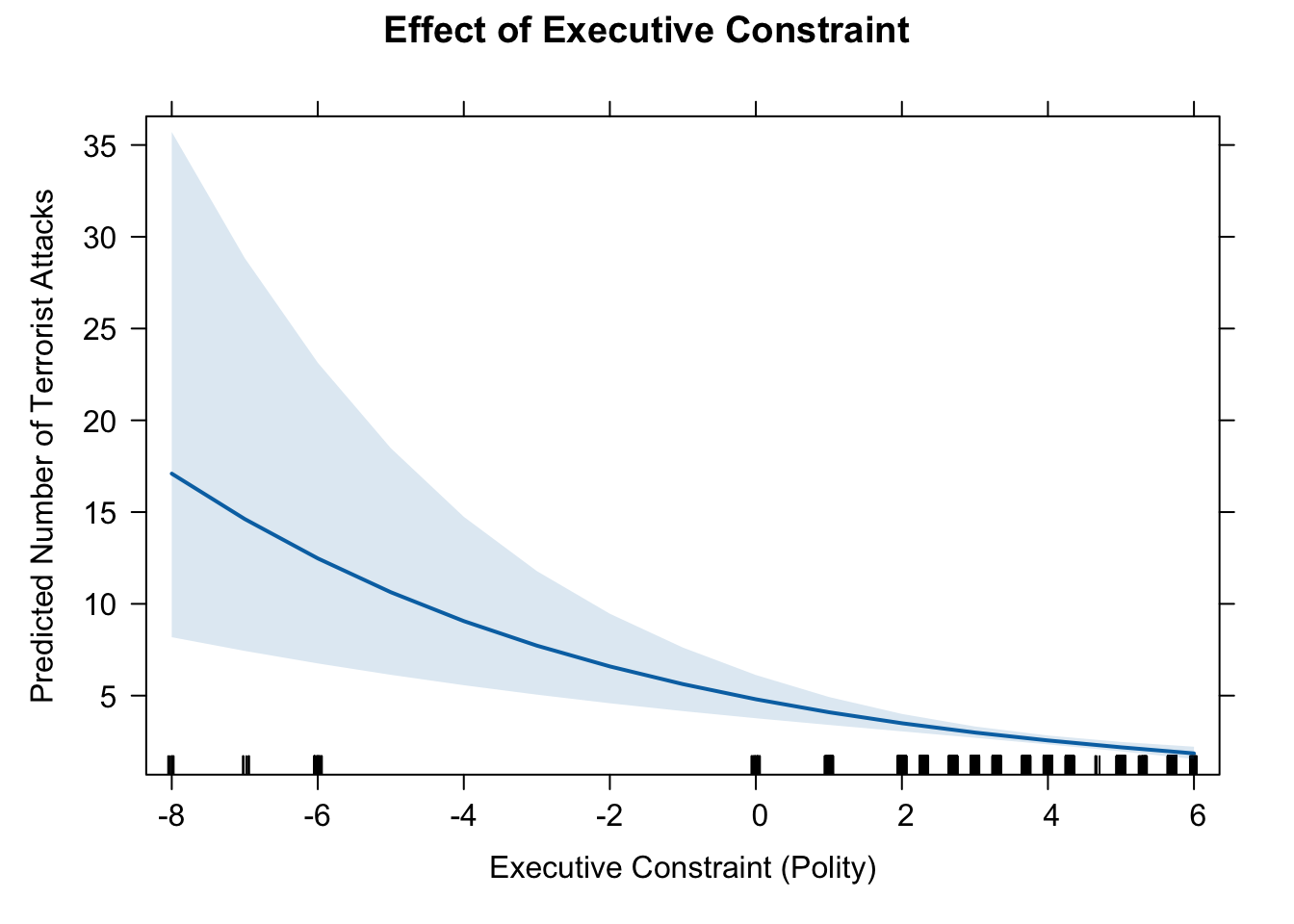
# dev.off()plot_model(fit.nb, type = "pred", terms = c("Executive [all]"), ci.lvl = 0.95, bpe.style = "line", robust = T, legend.title = "", vcov.type = c("HC3"), colors="bw") +
theme_bw() +
ggtitle(element_blank()) +
xlab("Effect of Executive Constraint") + ylab("Predicted Number of Terrorist Attacks") +
labs(title = "Effect Plot") +
theme(plot.title = element_text(hjust = 0.5)) 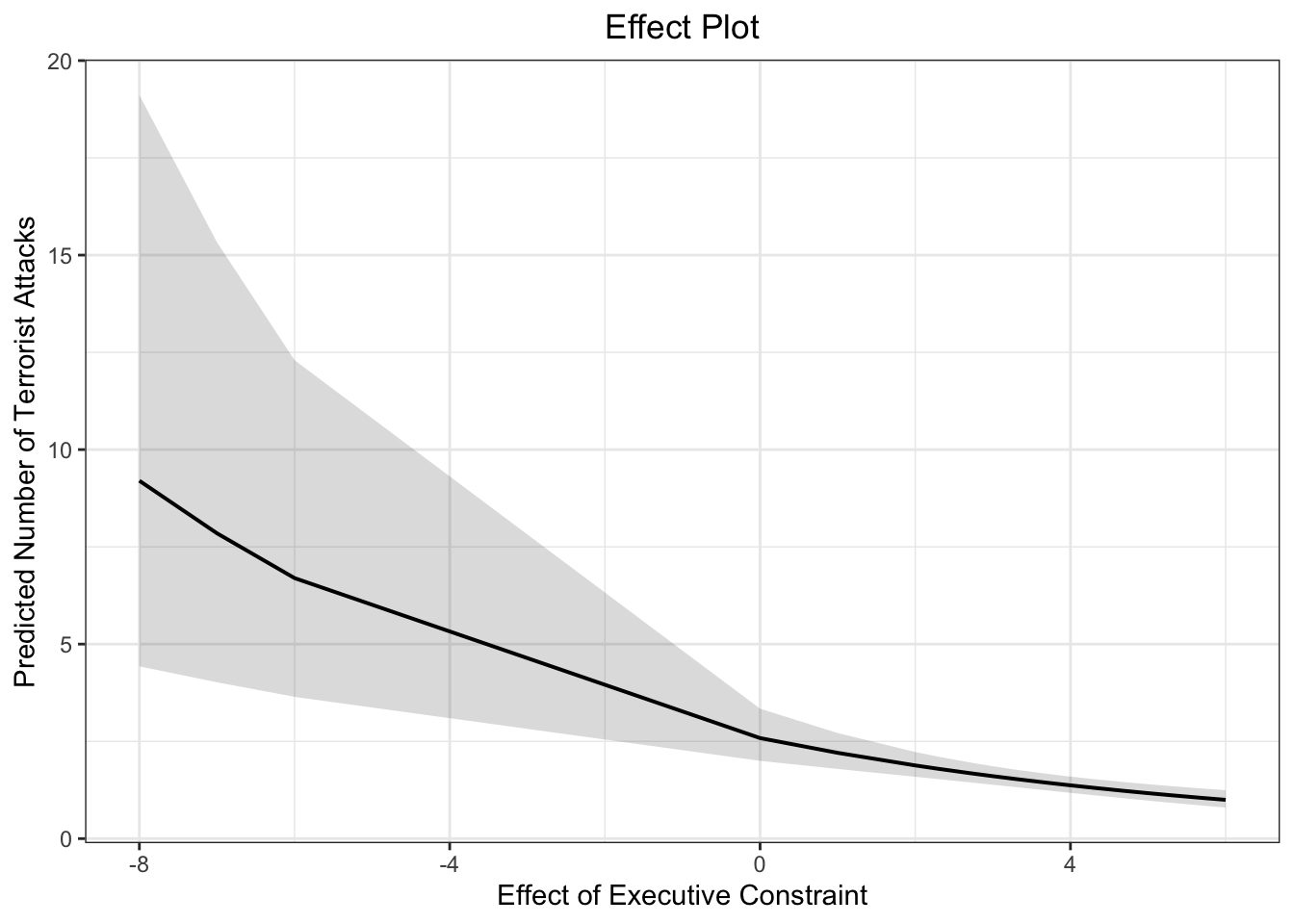
12. effect of GINI
eff.gini1 <- effect(term = "GINI", mod = fit.nb)
eff.gini1##
## GINI effect
## GINI
## 20 40 50 70 80
## 0.8928154 2.3933753 3.9186400 10.5047204 17.1992323# pdf(file = "eff_gini1.pdf", width = 10, height = 7)
plot(eff.gini1, type = "response",
main = "Effect of GINI Coefficient",
ylab = "Predicted Number of Terrorist Attacks",
xlab = "GINI Coefficient")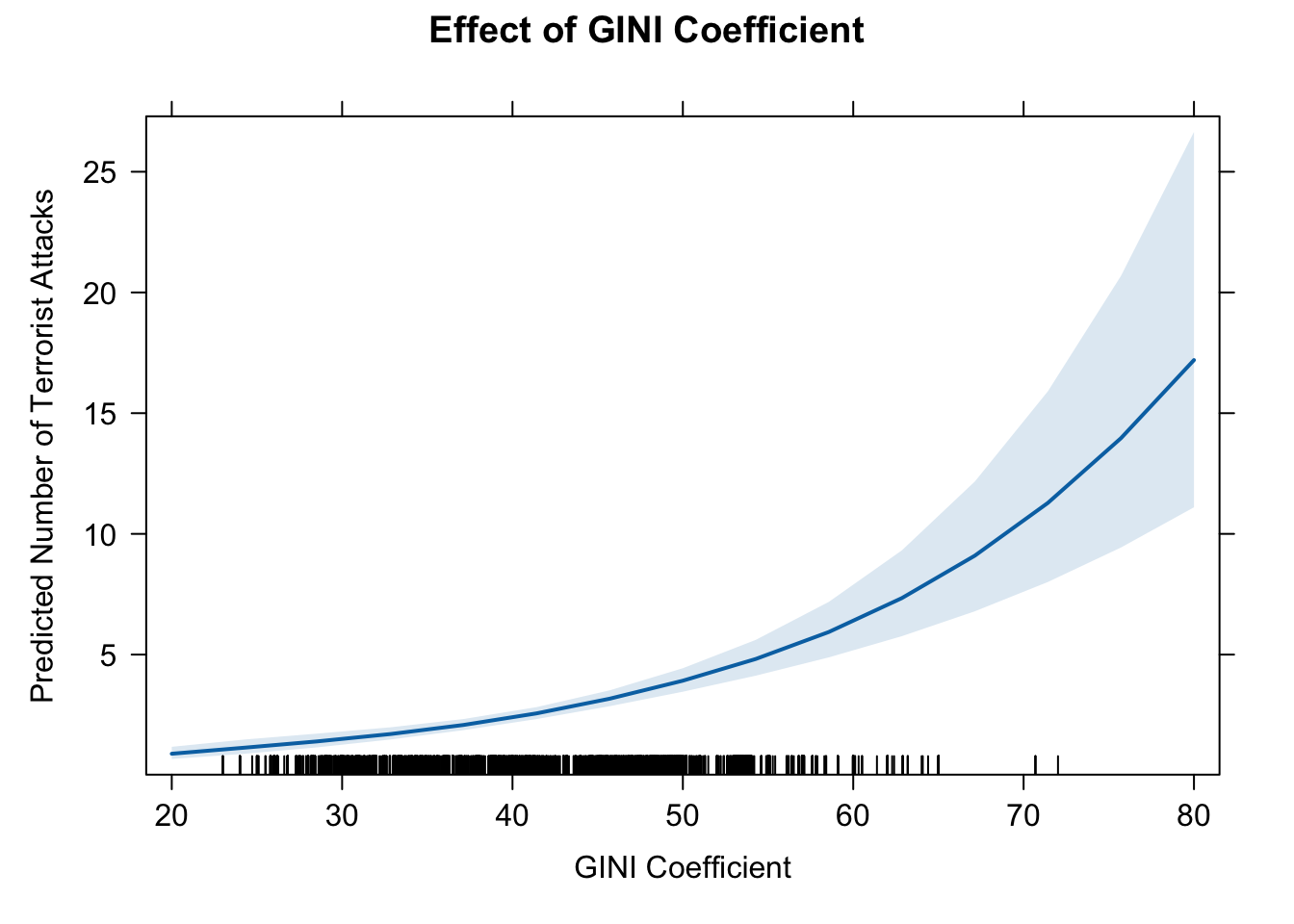
# dev.off()plot_model(fit.nb, type = "pred", terms = c("GINI [all]"), ci.lvl = 0.95, bpe.style = "line", robust = T, legend.title = "", vcov.type = c("HC3"), colors="bw") +
theme_bw() +
ggtitle(element_blank()) +
xlab("Effect of GINI Coefficient") + ylab("Predicted Number of Terrorist Attacks") +
labs(title = "Effect Plot") +
theme(plot.title = element_text(hjust = 0.5)) 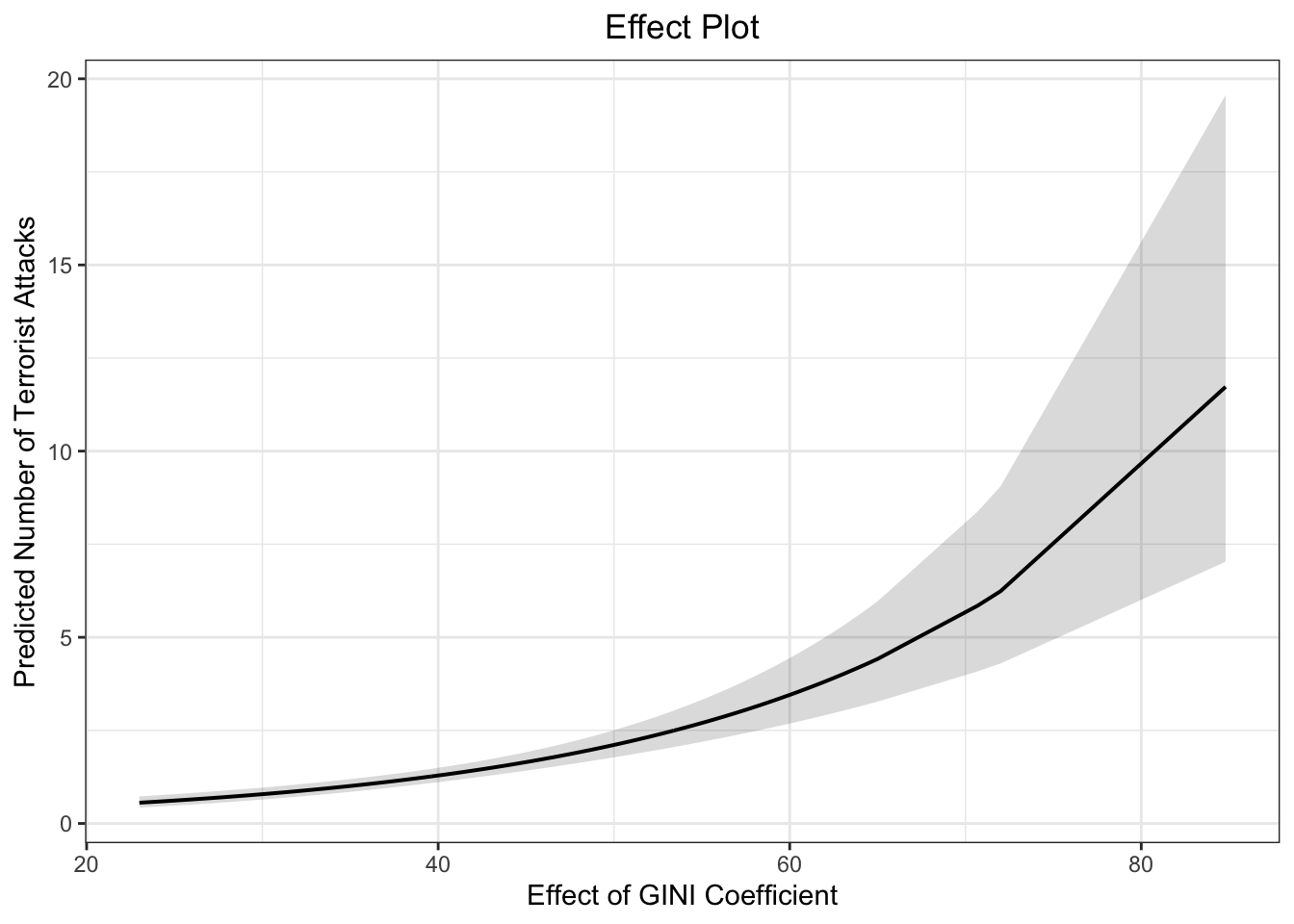
The estimates suggest that GINI coefficient has a positive effect on the number of domestic terrorist attacks.
13. Quadratic model
# (a): manually include a quadratic term
# create a quadratic term
att $ GINI2 <- att $ GINI^2
fit.nb2A <- glm.nb(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
laglogGNI + GINI + GINI2 + Partic + Executive ,
data = att)
# (b): include it using the I() function
fit.nb2B <- glm.nb(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
laglogGNI + GINI + I(GINI^2) + Partic + Executive ,
data = att)
# (c): compare the two
stargazer(fit.nb2A, fit.nb2B, type= "text")##
## ===================================================
## Dependent variable:
## ---------------------------------
## GTDDomestic
## (1) (2)
## ---------------------------------------------------
## lagECDIS23or4Yes 1.405*** 1.405***
## (0.101) (0.101)
##
## logpop 1.059*** 1.059***
## (0.046) (0.046)
##
## logarea -0.340*** -0.340***
## (0.035) (0.035)
##
## Durable -0.008*** -0.008***
## (0.002) (0.002)
##
## laglogGNI 0.219*** 0.219***
## (0.039) (0.039)
##
## GINI 0.225*** 0.225***
## (0.042) (0.042)
##
## GINI2 -0.002***
## (0.0005)
##
## I(GINI2) -0.002***
## (0.0005)
##
## Partic -0.298*** -0.298***
## (0.048) (0.048)
##
## Executive -0.170*** -0.170***
## (0.032) (0.032)
##
## Constant -3.387*** -3.387***
## (1.051) (1.051)
##
## ---------------------------------------------------
## Observations 2,964 2,964
## Log Likelihood -5,614.203 -5,614.203
## theta 0.189*** (0.007) 0.189*** (0.007)
## Akaike Inf. Crit. 11,248.410 11,248.410
## ===================================================
## Note: *p<0.1; **p<0.05; ***p<0.01# (d): compare the model that has a quadratic term and the one without it
stargazer(fit.nb, fit.nb2B, type= "text")##
## ===================================================
## Dependent variable:
## ---------------------------------
## GTDDomestic
## (1) (2)
## ---------------------------------------------------
## lagECDIS23or4Yes 1.457*** 1.405***
## (0.102) (0.101)
##
## logpop 1.082*** 1.059***
## (0.046) (0.046)
##
## logarea -0.348*** -0.340***
## (0.036) (0.035)
##
## Durable -0.009*** -0.008***
## (0.002) (0.002)
##
## laglogGNI 0.215*** 0.219***
## (0.040) (0.039)
##
## GINI 0.049*** 0.225***
## (0.006) (0.042)
##
## I(GINI2) -0.002***
## (0.0005)
##
## Partic -0.299*** -0.298***
## (0.049) (0.048)
##
## Executive -0.159*** -0.170***
## (0.032) (0.032)
##
## Constant 0.276 -3.387***
## (0.555) (1.051)
##
## ---------------------------------------------------
## Observations 2,964 2,964
## Log Likelihood -5,626.221 -5,614.203
## theta 0.185*** (0.007) 0.189*** (0.007)
## Akaike Inf. Crit. 11,270.440 11,248.410
## ===================================================
## Note: *p<0.1; **p<0.05; ***p<0.01# The AIC score is lower for the model that includes a quadratic term, so
# we should prefer that one. 14. effect of GINI based on model (a)
eff.gini2.wrong <- effect(term = "GINI", mod = fit.nb2A)
eff.gini2.wrong##
## GINI effect
## GINI
## 20 40 50 70 80
## 1.679565e-02 1.508759e+00 1.429984e+01 1.284560e+03 1.217491e+04# pdf(file = "eff_gini2_wrong.pdf", width = 10, height = 7)
plot(eff.gini2.wrong, type = "response",
main = "Effect of GINI Coefficient (incorrect calculation)",
ylab = "Predicted Number of Terrorist Attacks",
xlab = "GINI Coefficient")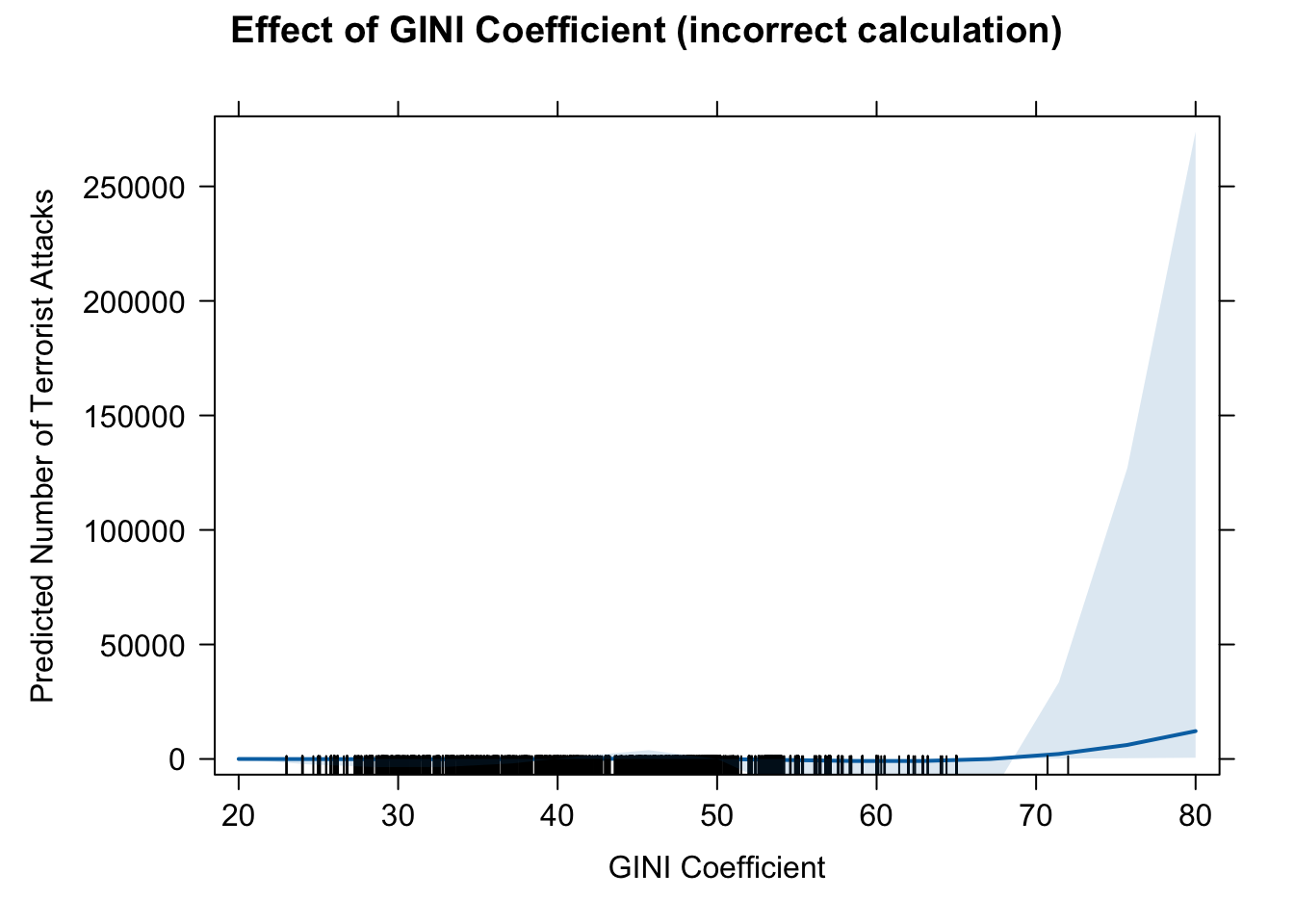
# dev.off()15. effect of GINI based on model (b)
eff.gini2 <- effect(term = "GINI", mod = fit.nb2B)
eff.gini2##
## GINI effect
## GINI
## 20 40 50 70 80
## 0.3489935 2.7356901 4.1629225 2.8475701 1.2800269# pdf(file = "eff_gini2.pdf", width = 10, height = 7)
plot(eff.gini2, type = "response",
main = "Effect of GINI Coefficient",
ylab = "Predicted Number of Terrorist Attacks",
xlab = "GINI Coefficient")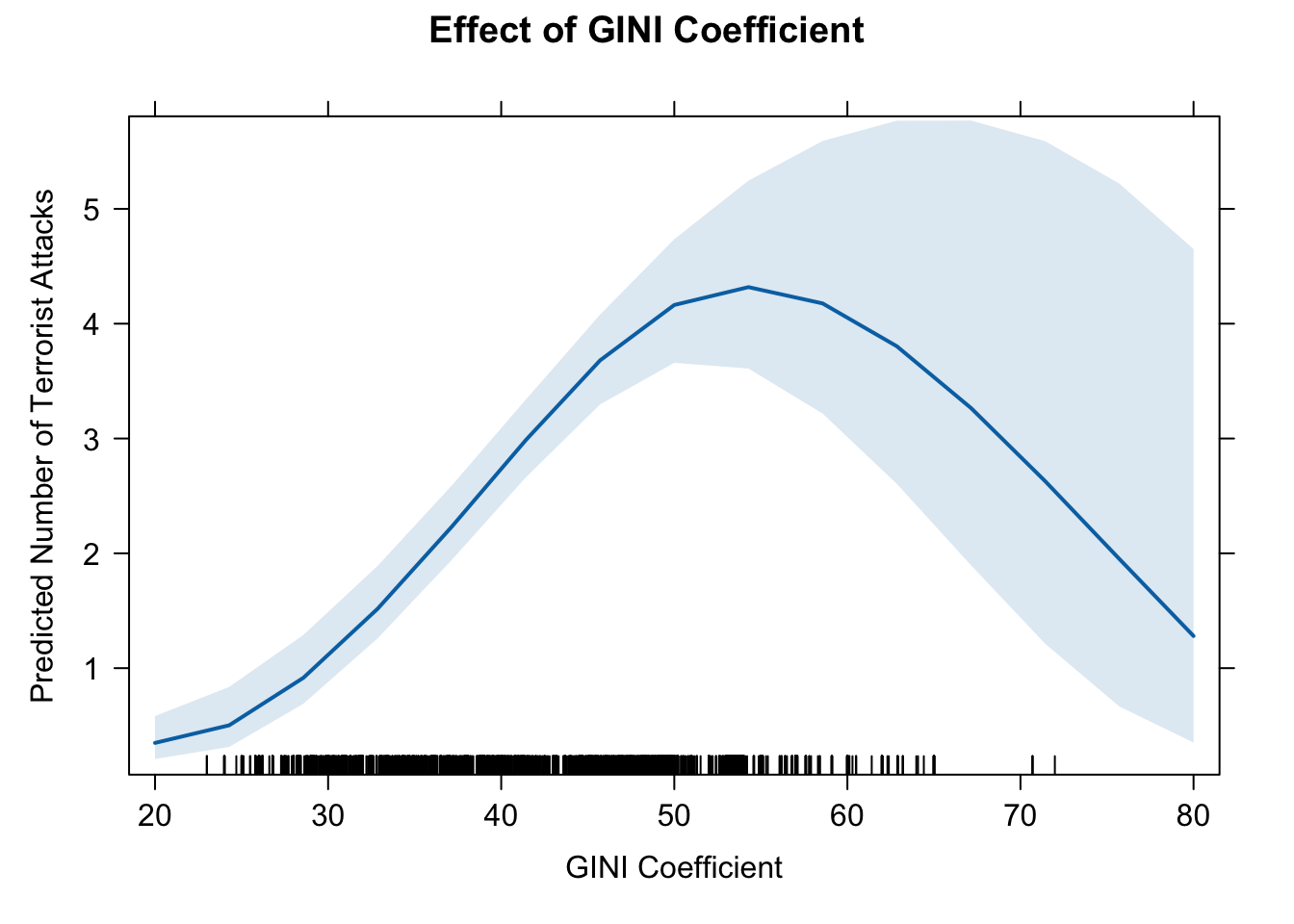
# dev.off()Zero-inflated NegBin
We may want to model the zero and nonzero processes separately and see how our predictors are correlated with these two processes.
m1 <- zeroinfl(GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable + # covariates for the count model
laglogGNI + GINI + Partic + Executive |
lagECDIS23or4 + logpop + logarea + Durable + # covariates for the zeroinf model
laglogGNI + GINI + Partic + Executive,
link="logit",
dist = "negbin",
data = att)
summary(m1)##
## Call:
## zeroinfl(formula = GTDDomestic ~ lagECDIS23or4 + logpop + logarea + Durable +
## laglogGNI + GINI + Partic + Executive | lagECDIS23or4 + logpop +
## logarea + Durable + laglogGNI + GINI + Partic + Executive, data = att,
## dist = "negbin", link = "logit")
##
## Pearson residuals:
## Min 1Q Median 3Q Max
## -0.44255 -0.42234 -0.36073 -0.08313 22.03807
##
## Count model coefficients (negbin with log link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.478192 0.611817 0.782 0.434453
## lagECDIS23or4Yes 1.301832 0.104469 12.461 < 2e-16 ***
## logpop 1.063907 0.053026 20.064 < 2e-16 ***
## logarea -0.436662 0.039925 -10.937 < 2e-16 ***
## Durable -0.006840 0.001813 -3.772 0.000162 ***
## laglogGNI 0.298991 0.046531 6.426 1.31e-10 ***
## GINI 0.059794 0.006872 8.701 < 2e-16 ***
## Partic -0.285409 0.049786 -5.733 9.88e-09 ***
## Executive -0.176544 0.028377 -6.221 4.93e-10 ***
## Log(theta) -1.629620 0.037936 -42.957 < 2e-16 ***
##
## Zero-inflation model coefficients (binomial with logit link):
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.87988 4.25748 0.911 0.36213
## lagECDIS23or4Yes -4.33123 1.59092 -2.722 0.00648 **
## logpop -0.35406 0.49255 -0.719 0.47224
## logarea -1.36335 0.44338 -3.075 0.00211 **
## Durable 0.05273 0.02000 2.636 0.00838 **
## laglogGNI 0.61602 0.33087 1.862 0.06263 .
## GINI 0.10181 0.04358 2.336 0.01947 *
## Partic -0.46593 0.44007 -1.059 0.28970
## Executive -0.38824 0.17756 -2.186 0.02878 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Theta = 0.196
## Number of iterations in BFGS optimization: 68
## Log-likelihood: -5587 on 19 DfWe see that economic discrimination on minorities are positively correlated with countries where attacks happen but negatively correlated with countries where attacks never happen.
Again, let’s plot the effect plots. plot_model doesn’t generate the hurdle- or zero-inflated models for some reason. We use ggpredict here.
Show the zero-inflation part of the model
g <- ggpredict(m1, terms="lagECDIS23or4")
g_bin <- plot(g) + theme_bw() +
ggtitle(element_blank()) +
xlab("Economic Discrimination") + ylab("Predicted Number of Terrorist Attacks") +
labs(title = "Effect Plot (count model)") +
theme(plot.title = element_text(hjust = 0.5))
g1 <- ggpredict(m1, terms="lagECDIS23or4", type="zi_prob")
g_count <- plot(g1) + theme_bw() +
ggtitle(element_blank()) +
xlab("Economic Discrimination") + ylab("Predicted Number of Terrorist Attacks") +
labs(title = "Effect Plot (binary response model)") +
theme(plot.title = element_text(hjust = 0.5))
library(ggpubr)
figure <- ggarrange(g_bin, g_count, nrow = 1) + theme_minimal(base_family = "Fira Sans", base_size = 18)
figure 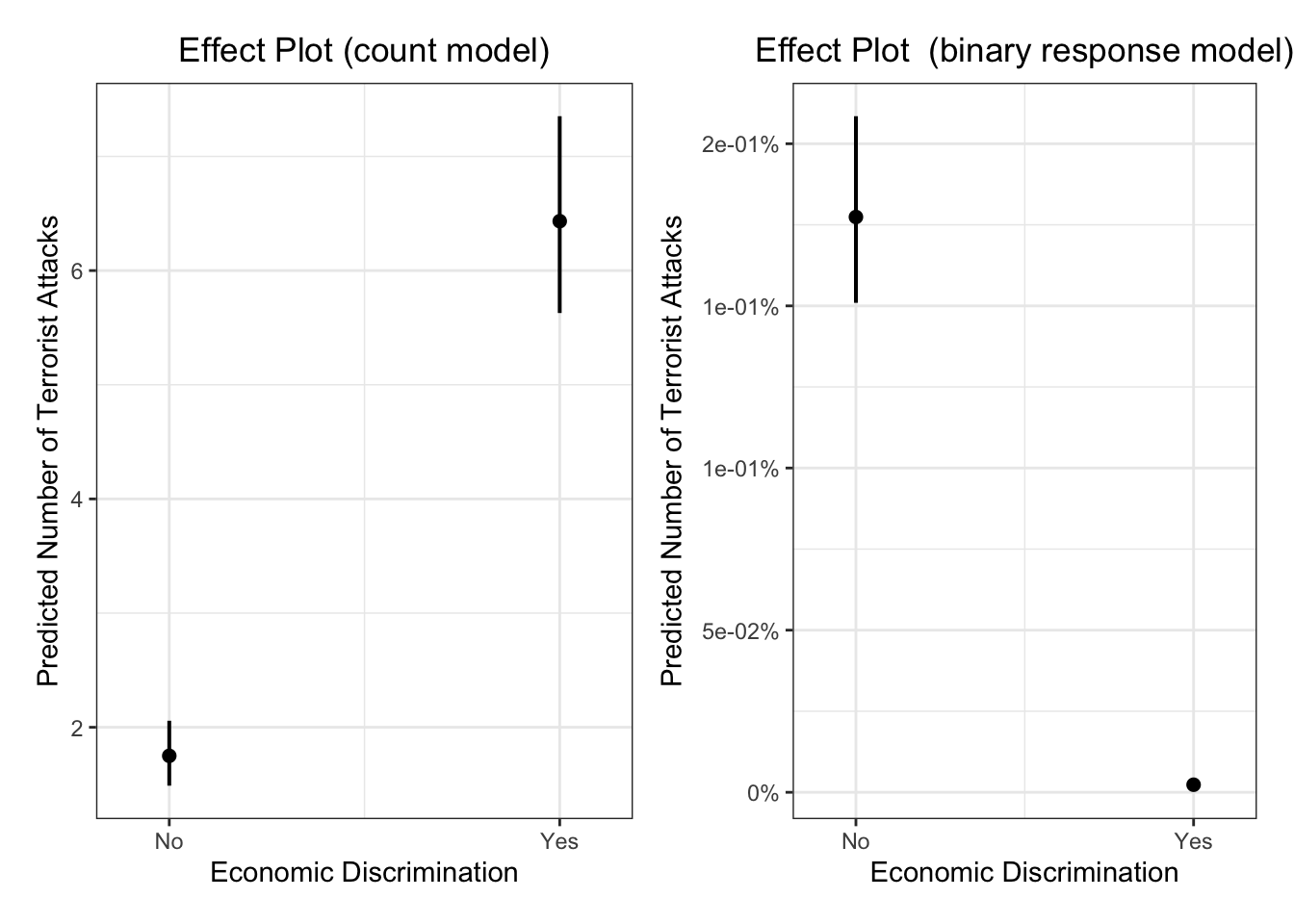
Descriptive Stats: bar chart
## Country code
att $ isocode <- countrycode(att $ Country, origin = "country.name", destination = "iso3c")## Warning: Some values were not matched unambiguously: Australi, Azerbaij, Banglade, Cape Ver, CentralA, Costa Ri, Coted'Iv, East Tim, ElSalvad, Equatori, Guatemal, Indonesi, Lithuani, Macedoni, Madagasc, Mauritan, Mauritiu, Mozambiq, Netherla, NewZeala, Nicaragu, NorthKor, Philippi, SaudiAra, Singapor, SouthAfr, SouthKor, Swazilan, United S, UnitedAr, UnitedKi, Venezuel, Yugoslavatt $ isocode[att $ Country == "GuineaBi"] <- "GNB"
att $ isocode[is.na(att $ isocode)] <- countrycode(att $ COW[is.na(att $ isocode)],
origin = "cown",
destination = "iso3c")## Warning: Some values were not matched unambiguously: 345, 361, 440, 699, 765att $ isocode[att $ Country == "Banglade"] <- "BGD"
att $ isocode[att $ Country == "Equatori"] <- "GNQ"
att $ isocode[att $ Country == "Lithuani"] <- "LTU"
att $ isocode[att $ Country == "UnitedAr"] <- "ARE"
att $ isocode[att $ Country == "Yugoslav"] <- "YUG"
att $ isocode[att $ Country == "Macedoni"] <- "MKD"
att $ isocode[att $ Country == "Azerbaij"] <- "AZE"
att $ isocode[att $ Country == "Uzbekist"] <- "UZB"
## Collapse this by country. That is, we calculate the sum of terrorist attacks for each country.
att.bycnt <- aggregate(GTDDomestic ~ Country + isocode,
data = att[c("GTDDomestic","Country","isocode")],
sum,
na.rm = TRUE)
summary(att.bycnt)## Country isocode GTDDomestic
## Length:172 Length:172 Min. : 0.0
## Class :character Class :character 1st Qu.: 6.0
## Mode :character Mode :character Median : 26.5
## Mean : 256.6
## 3rd Qu.: 123.0
## Max. :4612.0g <- ggplot(data = att.bycnt, aes(x = GTDDomestic)) + geom_histogram()
g## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.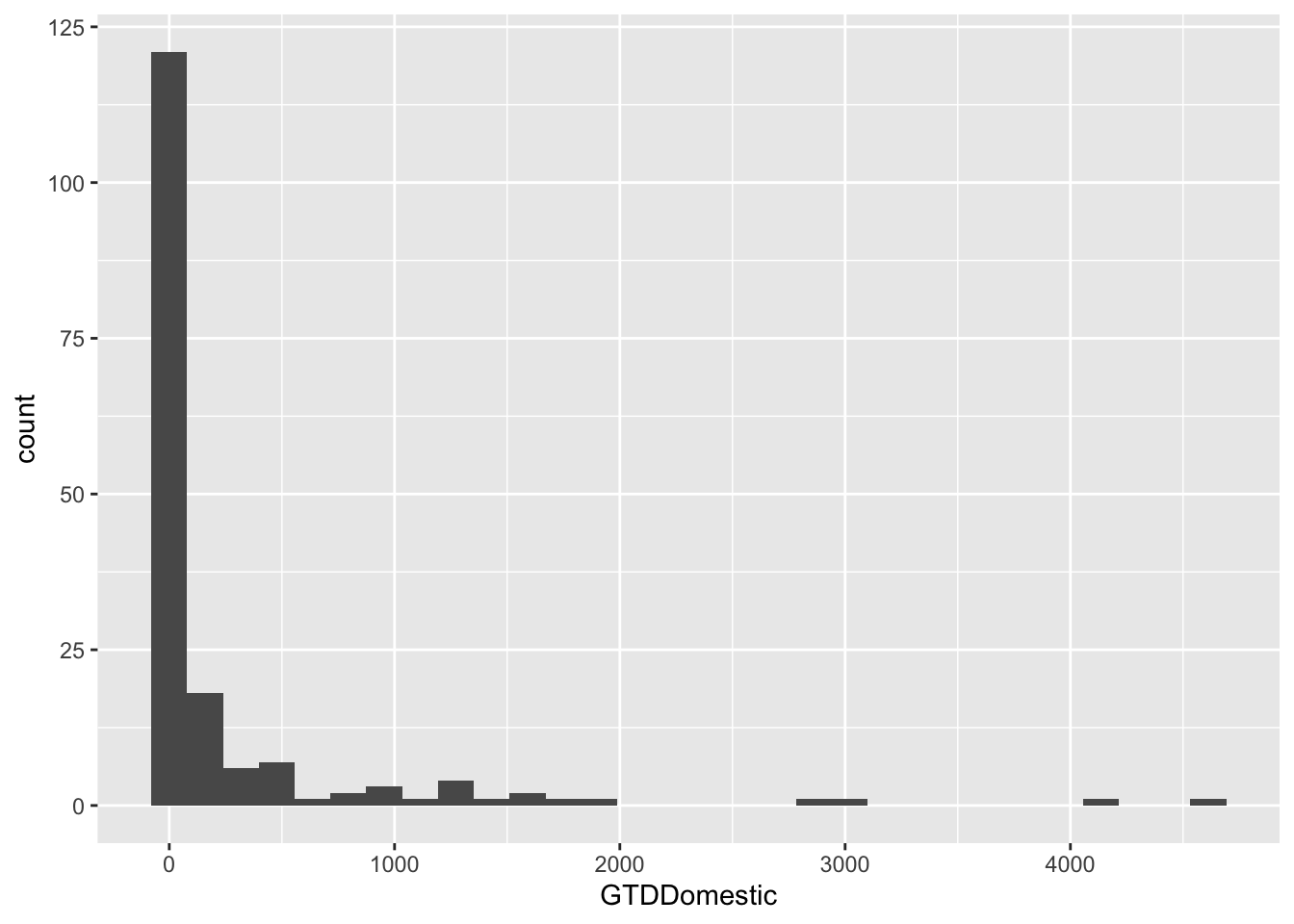
Descriptive Stats: map
Or examine the data on a map
## Maps
map.dat <- joinCountryData2Map(att.bycnt, # our data set
joinCode = "ISO3", # Declare that we use ISO 3-letter character code
nameJoinColumn = "isocode", # Specify the column containing joinCode
verbose = TRUE)## 171 codes from your data successfully matched countries in the map
## 1 codes from your data failed to match with a country code in the map
## failedCodes failedCountries
## [1,] "YUG" "Yugoslav"
## 73 codes from the map weren't represented in your data# mapDevice(device = "pdf", file = "map_terror.pdf", width=10, height=6)
mapCountryData(map.dat[map.dat$SOVEREIGNT != "Antarctica",], nameColumnToPlot = "GTDDomestic",
colourPalette = "terrain",
mapTitle = "Number of Terrorist Attacks, 1970-2006")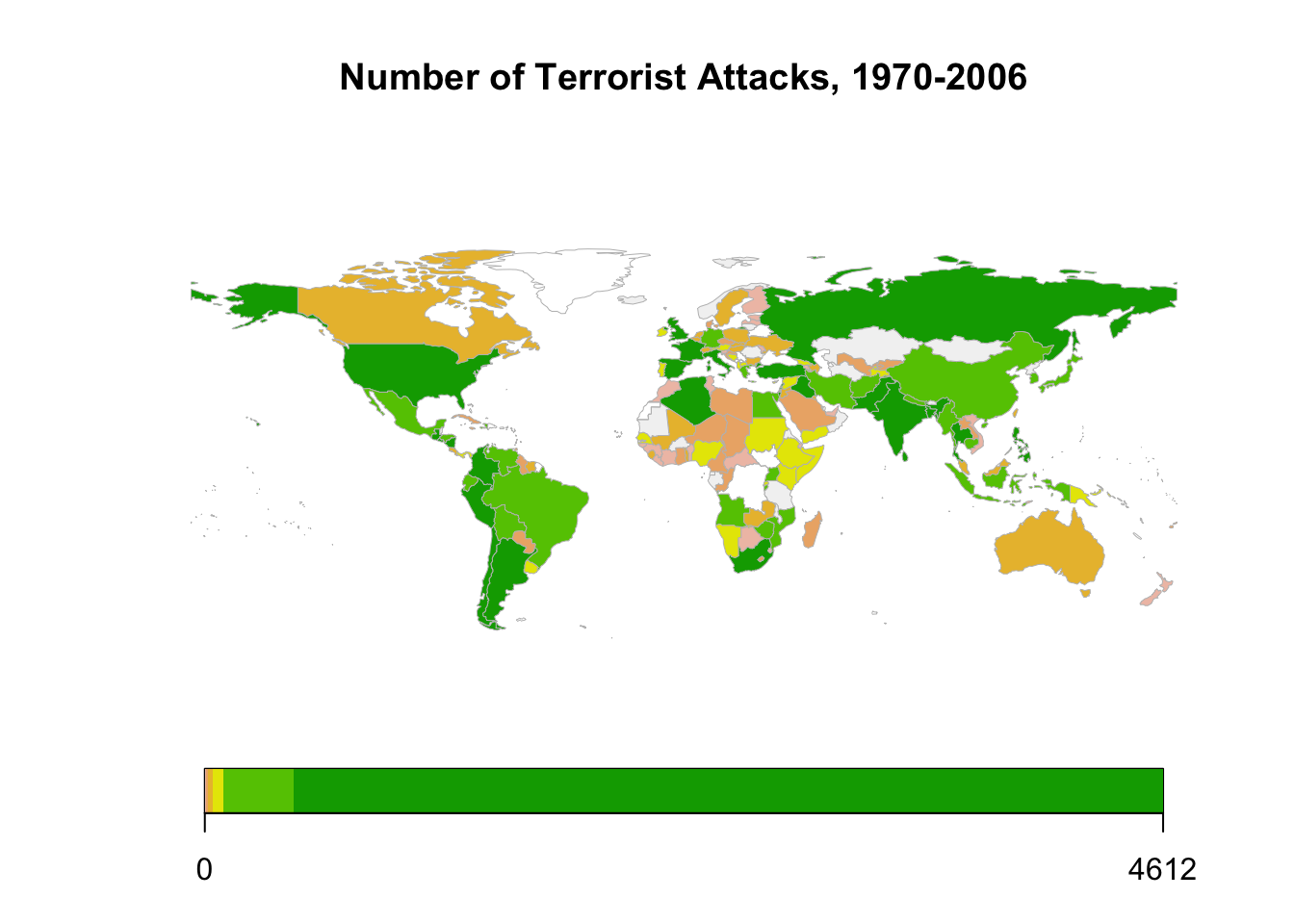
# dev.off()